Burger Bun
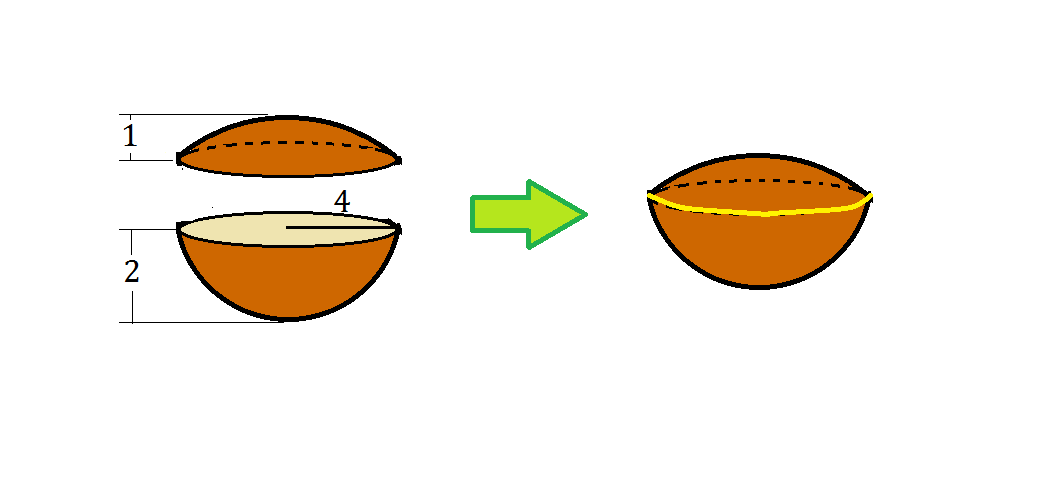
A new-styled burger bun is created by splicing 2 spherical dome-shaped bread pieces together, where both domes have got the same circle base of radius 4, such that only outer brownish surface is presented. One dome has the height of 1 while the other height of 2, as shown above.
What is the surface area of this burger bun? If your answer is in a form of , enter as your answer.
Note : Figure not drawn to scale.
The answer is 37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The formula for the curved surface area of a spherical cap is 2 π r h , where r is the radius of the sphere from which the cap is cut, and h is the height measured from the center of the base of the cap to its apex. We know the heights of the two caps are 1 and 2 ; we need to find their respective radii.
Let r and R be the radii of the spheres from which the top and bottom caps respectively were cut, as shown below.
( r − 1 ) 2 - 2 r + r = + 4 2 = r 2 1 7 = 0 2 1 7 ( R − 2 ) 2 - 4 R + R + 4 2 = R 2 2 0 = 0 = 5
Then the combined curved surface area of the two caps is 2 π ( 2 1 7 ) ( 1 ) + 2 π ( 5 ) ( 2 ) = 3 7 π