Burn Bright, Burn Fast
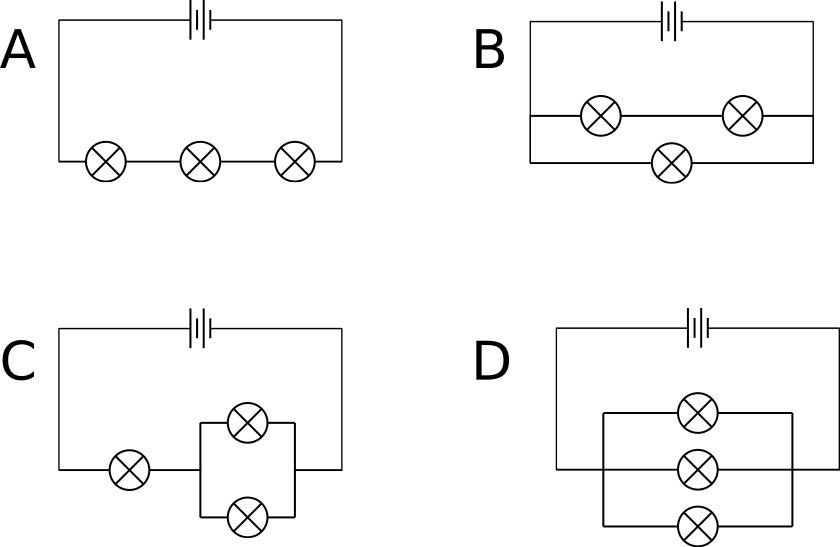
Ben has three bulbs and a battery. He can think of four different ways to connect the bulbs to the battery.
When connected to the circuit, the battery will eventually discharge. In which of the following arrangements will the battery discharge the fastest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we recall that the power output of a circuit is given by P = V I = V 2 / R . As the voltage is fixed by the strength of the battery, we can see that the circuit with the lowest resistance will have the greatest power dissipation.
A bulb in the circuit dissipates energy, and can be treated as a resistor. We can simplify the circuits by finding the effective resistances in each case. Suppose the resistance of each bulb is R .
Recall that
if resistors are connected in series, then their effective resistance is the sum of the individual resistors. R e f f = i ∑ R i .
if resistors are connected in parallel, then their effective resistance is the reciprocal of the sum of the reciprocals of the individual resistances. R e f f 1 = i ∑ R i 1
In circuit A, all three resistors are in series, so the effective resistance is the sum of resistances = 3 R .
In circuit B, two of the resistors are in series, and their effective resistance is 2 R . This effective resistor is in parallel with the third resistor R . Their effective resistance is 2 R / 3
In circuit C, two of the resistors are in parallel, and their effective resistance is R / 2 . This is in series with the third resistor, R and R / 2 are in series with each other. Their effective resistance is 3 R / 2 .
In circuit D, all three resistances are in parallel. Their effective resistance is R / 3 .
We see that the effective resistance is minimum in D. Since the voltage source is the same in all cases, current is the greatest in D. This implies in the same amount of time, more charge flows in circuit D than in the other three circuits, so the battery gets discharged the fastest in D.
Although the same components were used in all four circuits, the effective resistance, and therefore the current varies greatly depending on how the circuit is connected.