Burning candles
Three candles which can burn, 60 minutes, 80 minutes and 100 minutes respectively are lit at different times. All the candles are burning simultaneously for 30 minutes, and there is a total of 40 minutes in which exactly one is burning. For how many minutes are exactly two candles burning?
The answer is 55.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
So awesome
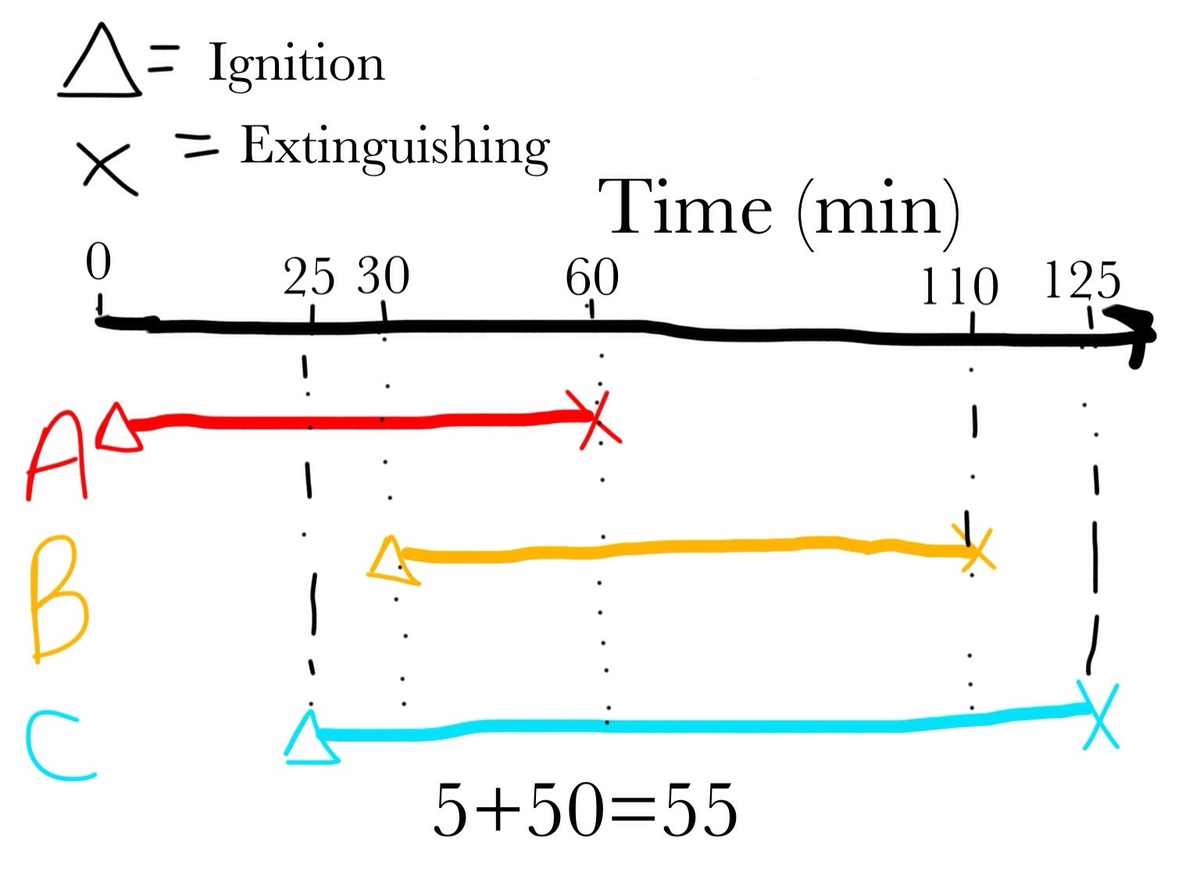
Here's a timeline setup. Take A, B, and C as the 60, 80, and 100 minute candles respectively.
Moderator note:
Very nice. How did you construct the time diagram? Is there only one solution?
The mathematical approach is the easiest. Total time is 1 0 0 + 8 0 + 6 0 = 2 4 0
Subtracting 3 × 3 0 = 9 0 when three candles burn together and 4 0 , when one candle burns alone, we get 1 1 0 minutes between two candles. Thus 5 5 . There is not one solution but several ways for the timeline to be created.
A ) Light 1 0 0 candle first at t = 0 , light 6 0 candle at t = 1 5 , light 8 0 candle at t = 4 5 .
B ) Light 8 0 candle first at t = 0 , light 1 0 0 candle at t = 2 5 , light 6 0 candle at t = 5 0 .
C ) Light 6 0 candle first at t = 0 , light 1 0 0 candle at t = 2 5 , light 8 0 candle at t = 3 0 .
Log in to reply
Alternative: Light 100 candle first, light 80 candle at 15, light 60 candle at 65. This is mirror solution to the original post.
Yes, only one solution: the total burning time is 60+80+100=240min. If they all burn together for 30min, that accounts for 30*3=90min. So with 90+40=130min accounted for, that leaves 240-130=110min to be accounted for with two candles burning simultaneously. Therefore, this happened for 110/2=55min.
Log in to reply
I considered 2 possibilities, the smallest is totally encompassed by the largest or the smallest has a portion outside the largest. It took just a few sketches to find both scenarios work, and both result with 55.
But wait, why does it not give t=30. Let's say 3 candles are a, b, c respectively. ! (n) is burning time. Time: 0 : a(0) 10: a(10), b(0) 30: a(30), b(20), c(0) 60: a(60), b(50), c(30) 30 minutes of 3 candles burning 90: b(80), c(60) 30 minutes of 2 candles burning 130: c(100) 40 minutes of one burning
The candles burn for a combined total of 240 minutes (60 + 80 + 100).
There's a 30 minute period where all 3 are burning simultaneously. This is a combined total of 90 minutes, leaving 150 minutes (240 - 150) remaining time where either 1 or 2 candles are burning.
The are 40 minutes where only 1 candle is burning. This leaves 110 minutes (150 - 40) total time where 2 candles are burning.
110 minutes total time / 2 candles = 55 minutes per candle.
Start with the 100 minute candle at t=0. Light up the 60 minute candle at t=15 minutes. Now light up the 80 minute candle at t=45 minutes. You will get answer =55 minutes, when exactly 2 candles burn. This is the EASIEST way the problem can be understood.
Denote each candles' burning time as T 1 , T 2 and T 3 .
The total burning time of all candles is T t o t = T 1 + T 2 + T 3 .
We will now consider the overlap time. I will denote this as O n , where n is the number of candles being overlapped. If n = 1 , then that's just one candle burning. We must arrive at the same burning time if write T t o t = 3 O 1 + 2 O 2 + O 1 . Hence T 1 + T 2 + T 3 = 3 O 3 + 2 O 2 + O 1 .
Since we are solving for O 2 = > O 2 = 2 1 ( T t o t − 3 O 3 − O 1 ) = 2 2 4 0 − 3 × 3 0 − 4 0 = 5 5
A more generic equation can be written as ∑ i = 1 n T n = ∑ i = 1 n n O n .