...but now it is a hedge...

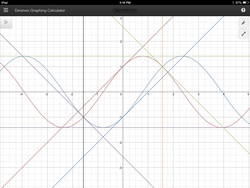A gardener with a keen interest in mathematics was very interested in the shapes made by the curves $\sin x + \cos x$ and $\sin x -\cos x$ , and wanted to make that shape on the hedges in the garden. He wants to make the 'bird' shape out of an hedge, which stretches to infinity on a Cartesian plane. The gardener can do an infinite number of cuts, but every cut is a line. Since he can't make curved cuts, he will not be able to make the shape perfectly, however, using straight cuts, he can make a figure as close to the original outline as possible. If he cannot cut into the 'bird', let the area of the figure he can create be $G$ .

Find $\lfloor G \rfloor$ . The first few cuts are shown in the diagram.

This is part of the Sinusoidal, Cosinusoidal series