Butterfly Effect
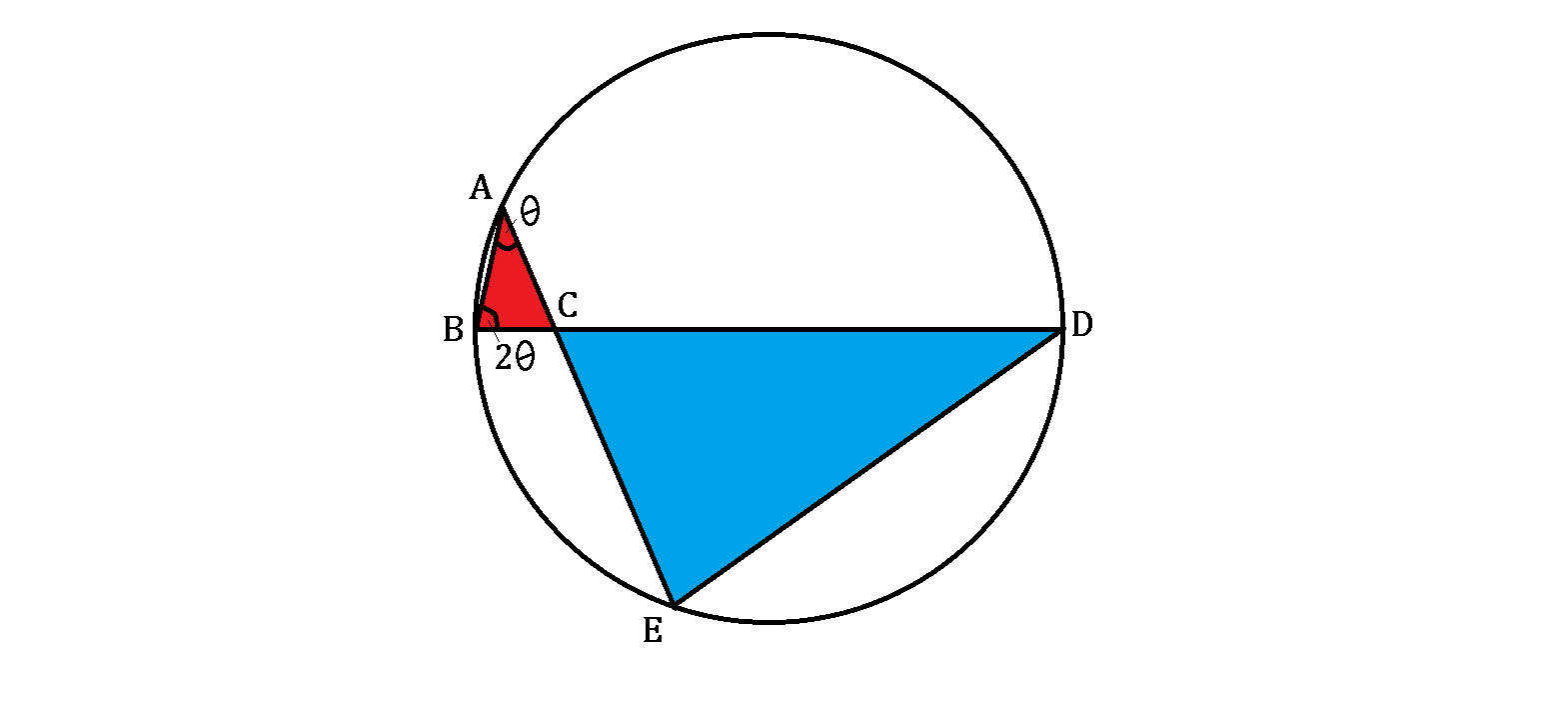
The lines above are drawn joining points A , B , D , E on the circumference of the circle, such that B D is a diameter of length 2 0 and ∠ A B C = 2 ∠ B A C .
If A C = 3 , what's the ratio of the areas of the two triangles, blue △ C D E to red △ A B C ?
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Did the same way.😁
Thank you! :)
Nice problem and elegant solution. I took a clumsy approach and focussed on θ , finding that the ratio of the blue to red areas is
6 cos ( 2 θ ) 4 0 cos ( θ ) − 3 such that 1 0 sin ( 3 θ ) = 3 sin ( 4 θ ) .
I'll remember to use the Intersecting Chords Theorem in the future. :)
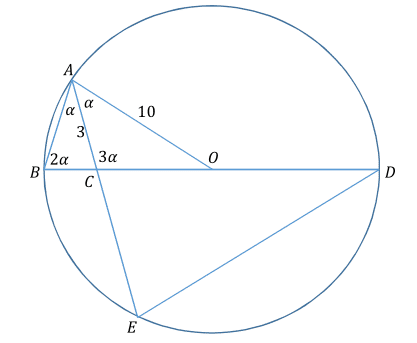 In
△
A
O
C
law of sines will give us
s
i
n
(
1
8
0
−
4
α
)
3
=
s
i
n
(
3
α
)
1
0
. This has only one positive solution under
4
5
∘
, namely
α
=
4
1
.
4
1
∘
.
In
△
A
O
C
law of sines will give us
s
i
n
(
1
8
0
−
4
α
)
3
=
s
i
n
(
3
α
)
1
0
. This has only one positive solution under
4
5
∘
, namely
α
=
4
1
.
4
1
∘
.
From △ A B C using law of sines we get B C = s i n ( 2 α ) 3 s i n ( α ) = 2 .
C D = 2 0 − B C = 1 8 , so the ratio of sides between the similar triangles A B D and D E C is 1 8 : 3 = 6 : 1 and the ratio of areas is 3 6 : 1 .
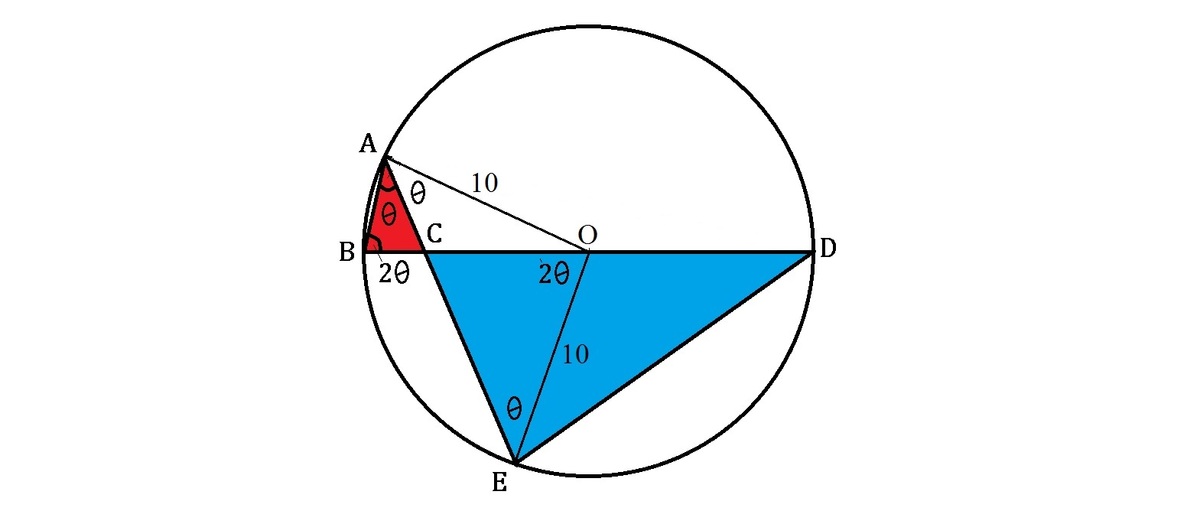
Let the centre of circle be O and B C = x . Using the sine rule on △ A B C , we have x sin θ = 3 sin 2 θ , ⟹ cos θ = 2 x 3 . Using the cosine rule on △ A C O , we have:
( 1 0 − x ) 2 1 0 0 − 2 0 x + x 2 x 2 − 2 0 x − 9 + x 9 0 x 3 − 2 0 x 2 − 9 x + 9 0 ( x − 2 ) ( x 2 − 1 8 x − 4 5 ) ⟹ x = 3 2 + 1 0 2 − 6 0 cos θ = 1 0 9 − 6 0 × 2 x 3 = 0 = 0 = 0 = ⎩ ⎪ ⎨ ⎪ ⎧ 2 2 0 . 2 2 5 − 2 . 2 2 2 accepted > 2 0 , rejected < 0 , rejected
Let the height of △ A B C be h . We note that △ E O C is similar to △ A B C . Since B C O C = 2 8 = 4 , then the height of △ E O C which is also the height of △ C D E , H = 4 h . Then, we have ratio of areas, A A B C A C D E = 2 1 B C ⋅ h 2 1 C D ⋅ H = 2 h 1 8 ⋅ 4 h = 3 6
We can also solve by finding cos(theta) which comes out to be 3/4.then the apply formula for area.
I don't understand what you're saying. How do you show that cos(theta) = 3/4?
And what formula for area are you referring to?
Relevant wiki: Two Secants
If we draw a radius joining point E and center O , we will obtain the center angle of ∠ C O E = 2 ∠ B A C according to Center Angle Theorem . Thus, ∠ C O E = ∠ A B C , and since ∠ A C B = ∠ E C O , the triangles A B C and C E O have the same internal angles and are, therefore, similar, as shown below: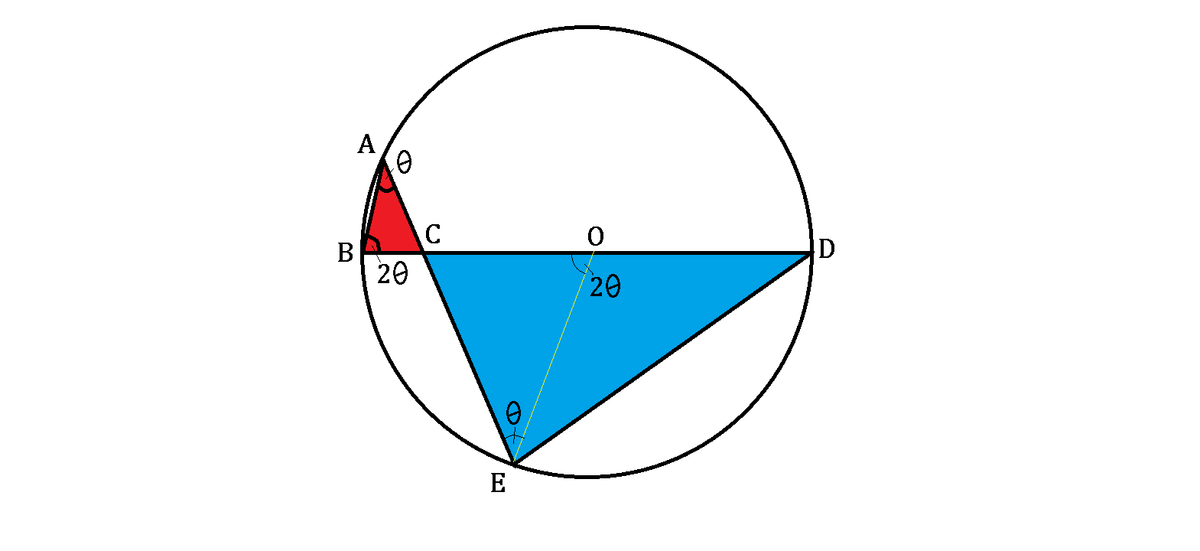
Now suppose B C = x and C E = y .
Then by similarity, 1 0 − x y = x 3 .
And according to Intersecting Chords Theorem , 3 y = x ( 2 0 − x ) .
Thus, 3 ( 1 0 − x ) = 3 x 2 ( 2 0 − x ) .
9 0 − 9 x = 2 0 x 2 − x 3
x 3 − 2 0 x 2 − 9 x + 9 0 = 0
( x − 2 ) ( x 2 − 1 8 x − 4 5 ) = 0
Thus, x = 2 because the other positive root exceeds 2 0 , which is the diameter length, while the other one is negative.
Then 3 y = 2 ⋅ 1 8 = 3 6 . Thus, y = 1 2 .
As a result, the side ratio of C E : A C = 1 2 : 3 = 4 : 1 .
Hence, the area ratio of △ C E O : △ A B C = 1 6 : 1 .
Then, since △ C E O and △ O D E share the same height with respect to the diameter chord, where C O : O D = 8 : 1 0 = 4 : 5 , the area ratio of △ C E O : △ O D E = 4 : 5 .
That is, △ C E O : △ O D E : △ A B C = 1 6 : 2 0 : 1 .
Finally, the area ratio of △ C D E : △ A B C = 3 6 : 1 .