[C] Question 5: Intermediate combinatorics
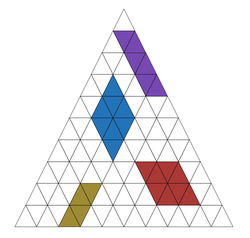How many parallelograms can be found in an equilateral triangle with side length 10 divided into equilateral triangles that each have side length 1?
The answer is 1485.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Try to find the number of llelograms this way:
1 x 1 = 45 1 x 2 = 36 1 x 3 = 28 1 x 4 = 21 1 x 5 = 15 1 x 6 = 10 1 x 7 = 06 1 x 8 = 03 1 x 9 = 01
It totals to 165. The same way, the sums of number of parallelograms "2 x 1, 2x2, 2x3...", "3x1, 3x2, 3x3..."... "9x1" are 120, 84, 56, 35, 20, 10, 04, 01 respectively.
Summing all these, we get 495.
And as the parallelograms are distinct from different vertices, we should multiply it with 3.
495 * 3 = 1485.
Here is another way to look at it. There are 66 vertices in the above triangle. Notice 11 on the bottom row, and 10 above, all the way to the single vertex on the top. Add these up, or use the formula
i = 1 ∑ n i = 2 n ( n + 1 )
Substituting n = 1 1 , we get 66.
Now, notice that each vertex is the intersection of three lines; one horizontal, one on the / line, and one on the \ line.
If you take any two vertices that do not share any lines, then these two vertices will uniquely define a parallelogram by inscribing the triangles between them. So, we just need to come up with a formula for all the ways we can pick two points that do not share a line.
First, the total number of points is 66, so there are ( 2 6 6 ) ways to pick two unique points.
Next, notice that if you select any random point, there are 20 vertices that share a line with it. This is true for any vertex. To see this, start with a vertex in the middle and move up and to the right one vertex along the / line. Now, you are on the same / line, so the number of vertices shared on that line stays the same. On the horizontal line, you now have one less because you moved up one row. On the \ line, you are now 1 more because you moved closer to the large right hand side. Thus, you only need to count the shared vertices for one vertex, and it is the same for them all - 20!
So, the number of ways to pick two vertices on the same line will be 2 6 6 × 2 0 . We need to include the 2 in the denominator since the two vertices can be in either order and the order we pick them is irrelevant. Thus, there are 660 ways to choose 2 points that share a line.
Plugging this into our original numbers, we get:
( 2 6 6 ) − 6 6 0 = 2 1 4 5 − 6 6 0 = 1 4 8 5
But by extending the base to 12 points, aren't you creating extra parallelograms?
Log in to reply
The points on the base are important. We ignore the other parallelograms created. Choose any 4 points on this base and we will define a parallelogram. Even if 4 consecutive points are chosen, the parallelogram defined is still in the original equilateral triangle.
i didn't get :(
Log in to reply
Sorry. I'm not very good at explaining.
Here's a link for a better explanation: Parallelograms in Triangles
Hi can you please explain" For easier calculation, we extend the triangle to have a base of 12 points. Then, those parallelograms will be defined by 4 points on this new extended base." sir :) ?
Consider any pair of distinct points in the triangle that do not both lie on one of the drawn lines. Label one of the points "1" and label the other point "2". If we can travel from 1 to 2 with only moves going to the right (it may go up at the same time), we can create a parallelogram. To do so, we first trace a path from 1 to 2 by only moving right (and not up) until we can go from the new point to 2 by only making moves that go up and right at the same time. This creates 2 sides of the parallelogram. To create the other 2 sides, we can either translate the 2 sides we have created or perform the 2 steps in the opposite order.
We will now prove that for any pair of distinct points that do not lie on a drawn line, we can rotate and/or relabel the points in exactly 1 way so that we can construct a parallelogram as above.
For any point, highlight the lines in the triangle that go through it. This should break up the original triangle into 3 equilateral triangles and 4 parallelograms (some of which may be degenerate). Given that we can rotate the triangle so that any base we want is the bottom base, it is clear that if this point is to be labeled 1, we can construct a parallelogram as above if and only if 2 is in one of the triangles.
Now suppose 2 is in one of the triangles, Then, the parallelogram opposite the triangle 2 is in "expands" to a parallelogram formed when the lines through 2 are drawn, and therefore contains 1. Therefore, 1 is not in one of the triangles for 2.
However, if 2 is in one of the parallelograms, then the triangle opposite the parallelogram "expands" to a triangle when the lines are drawn through 2, and therefore contains 1.
Therefore, either 1 is in one of the triangles for 2 or 2 is in one of the triangles for 1, but not both. Hence, exactly one rotation and labeling works.
Now, we will prove that any parallelogram can be defined by 2 such points. Consider the vertices with angles of 60 degrees. Clearly, these points work.
Therefore, the number of parallelograms is the number of ways to choose 2 distinct points that are not both on any drawn line. This is the number of pairs of distinct points - the number of pairs of distinct points that are both on a drawn lines, which is ( 2 6 6 ) − 3 ( ( 2 1 1 ) + ( 2 1 0 ) + ( 2 9 ) + … + ( 2 1 ) , which by the hockey stick pattern is ( 2 6 6 ) − 3 ( ( 3 1 2 ) = 1 4 8 5 .
This is a very similar question to finding the number of rectangles in 8 by 8 chessboard.
Look at the parallelograms. What are they defined by?
Two pair of parallel lines. Take a look at the blue parallelogram. Trace the two pair of parallel lines and you can see that 4 points on the base of the triangle will define that blue parallelogram.
Parallelograms whose vertice touch the base will be define by only 3 points. For easier calculation, we extend the triangle to have a base of 12 points. Then, those parallelograms will be defined by 4 points on this new extended base.
So 12C4?
No, the blue parallelogram has sides that are not parallel to the base of the triangle thus, it can be defined by the points on the base. The red parallelogram, however, cannot be defined by points on the base.
However, we can see that the red parallelogram can be defined by points on the other side of the triangle. We have to count the number of parallelograms that can be defined by points on each side of the triangle.
Thus, 3 × ( 4 1 2 ) = 1 4 8 5 .