Pretty Yellow Petals
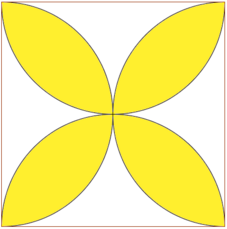 The figure above shows a square with side length,
a
. Find the area of the yellow region in terms of
a
.
The figure above shows a square with side length,
a
. Find the area of the yellow region in terms of
a
.
Hint : Circumcentre of each semicircle is midpoint of the square's side.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Put yellow area =y ,white area=w ,,,, so 4y+4w=square area=a^2,,,,,, 2y+w=semi.circle=πa^2\4\2=πa^2\8,,solve2equation,yellow area=a^2(π\2-1)=a^2\2(π-2)####
Simple yet best explanation Thanks Keep up the good work!
Find the area of the square and subtract that from the sum of the area of 4 semicircles.
The combined area of these semicircles should be greater than the square as its areas fill the region and also overlap each other. These petals are merely the areas that must overlap so that the semicircles can fill the figure. For these semicircles to fit the figure, they must share these regions of overlap.
As such, the area of the petals subtracted from the area of the semicircles should equal to the area of the square.
Alternatively, you can eliminate a pair of semicircles and then halve the square from the centre into two rectangles, each encasing a whole semicircle. Then, you could find the area of each rectangle and subtract the area of the semicircles from them. Multiplying this area by 4 gives you the area of the areas that are not petals, which you can then subtract from the area of the square.
One side =a
Diameter of circle = a
Area of half circle = πa^2/4*1/2 = πa^2/8
Draw 2 lines from 2 end points of side to the centre to form a triangle.
Now the height of the triangle is a/2
Area of the triangle = ½ a a/2 = a^2/4
Area of 2 half of 2 yellow part = Area of half circle – Area of the triangle
= πa^2/8 - a^2/4
= a^2/4(π/2-1)
Total area of yellow parts = 4*a^2/4(π/2-1)
= (π/2-1)*a^2
So to find the area of the shaded regions we essentially have to find the area of the square minus the white areas. We can find the area of two of the four white areas by subtracting out two of the semicircles(or one full circle). We then double that to get the full white area, and then subtract that from the square to get the yellow area.
Area of the square: a 2
Area of the circle: π ( 2 a ) 2 = π 4 a 2 = 4 π a 2
Subtracting to get two white areas: a 2 − 4 π a 2 = a 2 ( 1 − 4 π )
Double that to get entire white area(keeping things in terms of a^2): a 2 ∗ 2 ( 1 − 4 π ) = a 2 ( 2 − 2 π )
Subtract the white area from the square to get the yellow area:
a
2
−
a
2
(
2
−
2
π
)
=
a
2
(
1
−
(
2
−
2
π
)
)
=
a
2
(
1
−
2
+
2
π
)
=
a
2
(
2
π
−
1
)
Now, this answer isn't quite in the format of any of the choices, so we need to factor out 1/2 from ( 2 π − 1 ) , so that we can have a full π in the answer = a 2 ∗ 2 1 ( π − 2 ) = 2 a 2 ( π − 2 )
Solution:
We can detect quartercircle with B as a circumcentre. Segments A B and B C are equal and they are 2 a . An area of the quartercircle is 1 6 a 2 π . It is calculated easily that area of △ A B C is 8 a 2 . When we subtract triangle's area from quartercircle's area, we will have an area that is a half of one "petal", which is 1 6 a 2 ( π − 2 ) . To reach the area of four "petals", this latter area will need to be multiplied by 8. So, the solution would be 2 a 2 ( π − 2 ) .