Calculate the area of the yellow region and blue region
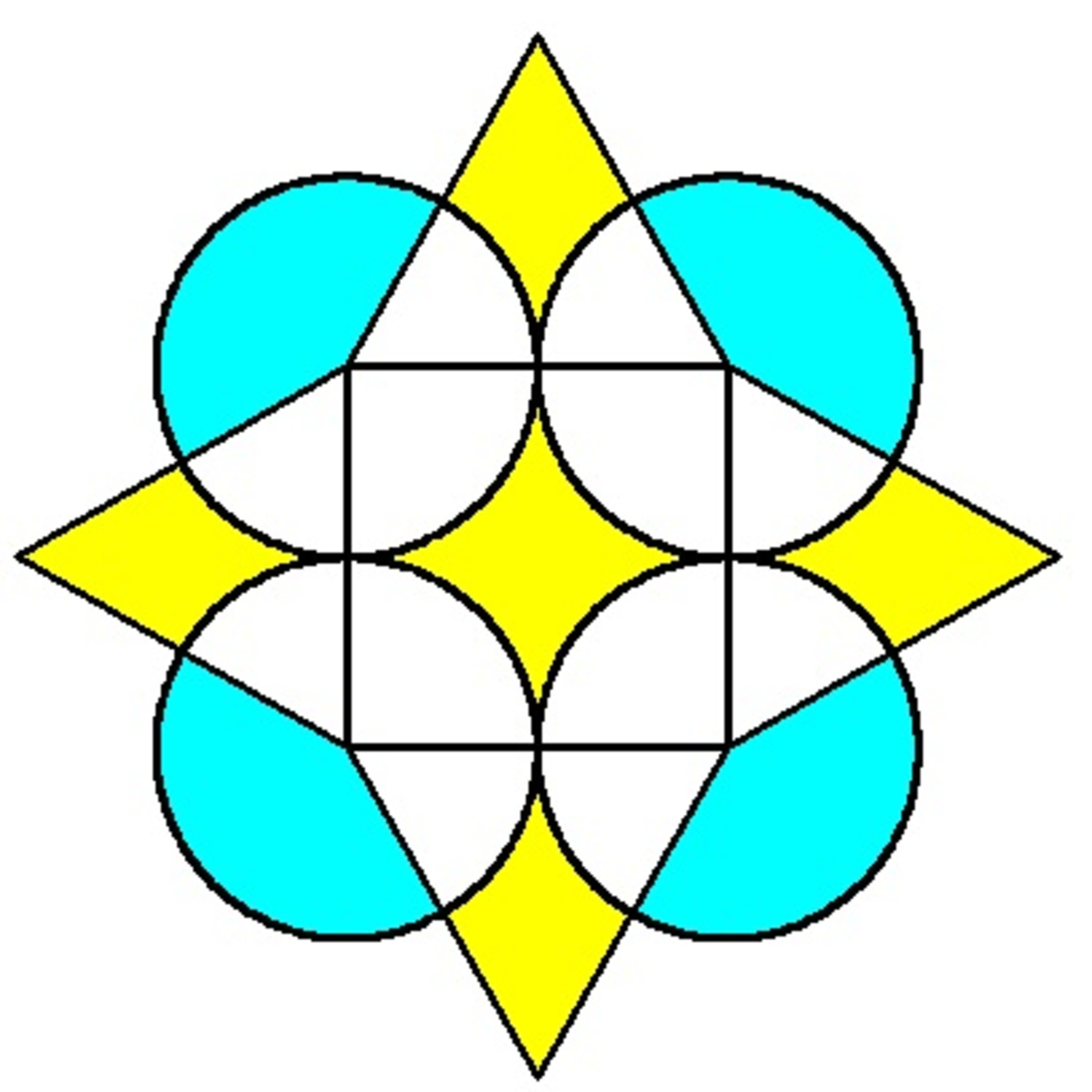 Four identical circles, each of radius
, are drawn on the vertices of a square whose side is
. Then four identical equilateral triangles are drawn as shown in the figure. Find the total area of the yellow region and blue region.
Four identical circles, each of radius
, are drawn on the vertices of a square whose side is
. Then four identical equilateral triangles are drawn as shown in the figure. Find the total area of the yellow region and blue region.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
y 1 = 6 2 − π ( 3 2 ) = 3 6 − 9 π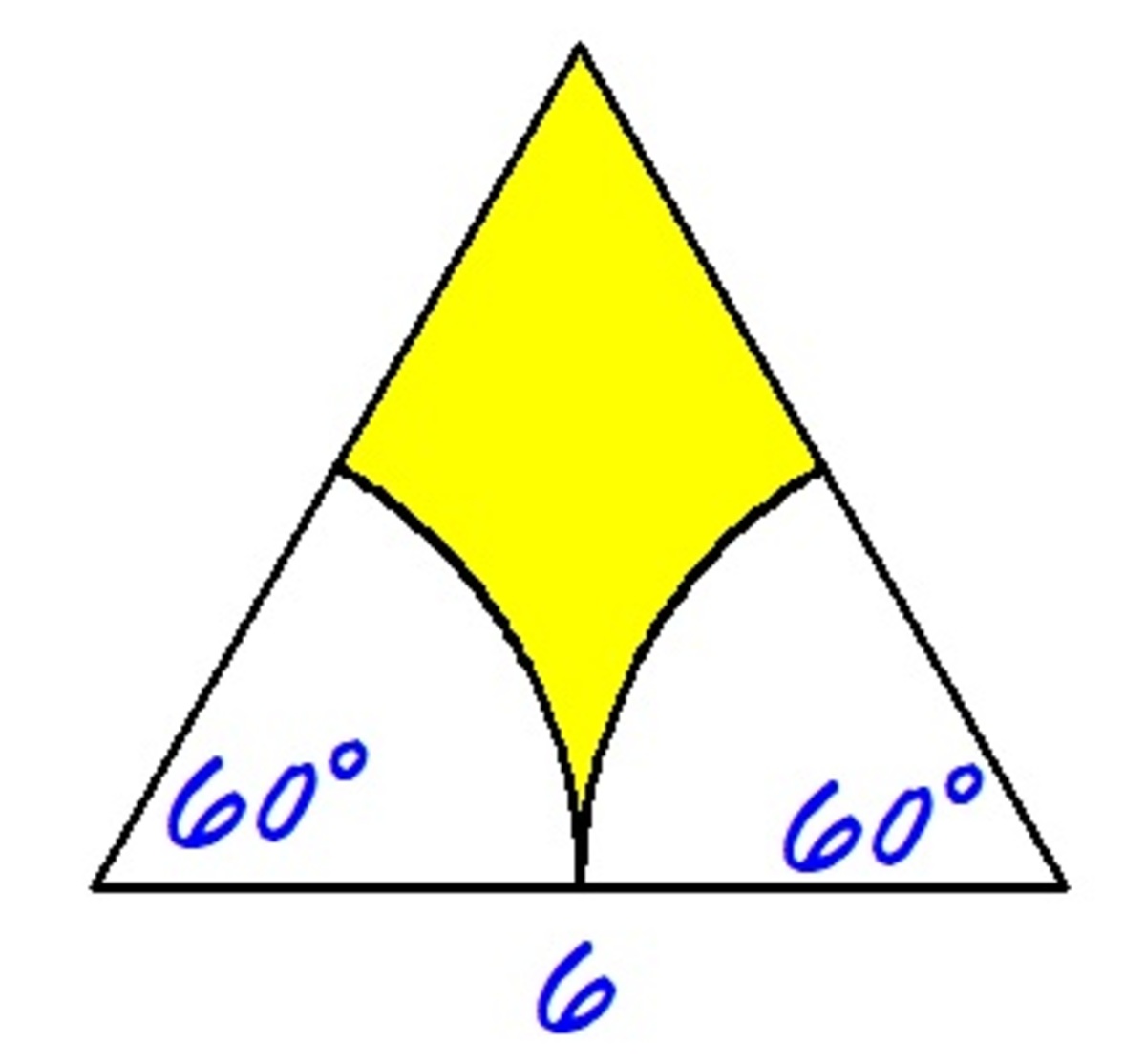
The area of the yellow region on each equilateral triangle can be computed as: area of an equilateral triangle minus area of two circular sectors then multiply it by 4 . We have
y 2 = 4 [ 4 3 ( 6 2 ) − 2 ( 3 6 0 6 0 ) ( π ) ( 3 2 ) ] = 3 6 3 − 1 2 π
The blue region is composed of four circular sectors having a central angle of 1 5 0 ∘ each. So the area is
b = 4 ( 3 6 0 1 5 0 ) π ( 3 2 ) = 1 5 π
The desired answer is 3 6 − 9 π + 3 6 3 − 1 2 π + 1 5 π = 3 6 + 3 6 3 − 6 π