Calculate the flux
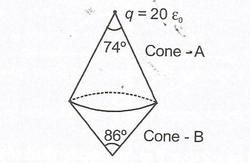 A point charge
is placed at the vertex of an imaginary cone, cone-A, as shown in the figure above. Find the magnitude of the electric flux through the curved surface of the other cone, cone-B, sharing its base with cone-A.
A point charge
is placed at the vertex of an imaginary cone, cone-A, as shown in the figure above. Find the magnitude of the electric flux through the curved surface of the other cone, cone-B, sharing its base with cone-A.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The flux through curved surface of cone B is same as the flux through the base, as cone B encloses no charge. Hence required flux is given by:
ϕ E = 2 ϵ 0 2 0 ϵ 0 ( 1 − cos ( ( 7 4 / 2 ) ∘ ) ) ≈ 2 N m 2 / C
Note: The electric flux through a disk due to the E field of a point charge q kept on its axis, such that the cone formed by the point and circumference has half angle θ is given by:
ϕ E = 2 ϵ 0 q ( 1 − cos θ )