Calculate this awesome limit!
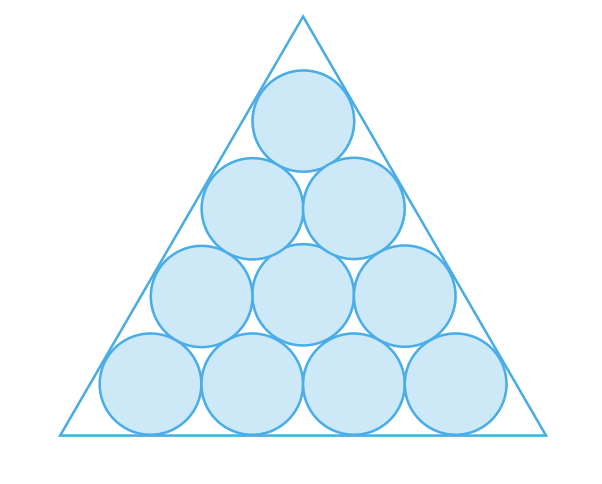
Suppose that circles of equal diameter are packed tightly in n rows inside an equilateral triangle. If A is the area of the triangle and B is the total area occupied by the n rows of circles, then find the limit of the ratio A B (correct to 3 decimal places) as the value of n approaches infinity.
The above figure shows the case for n = 4
*Courtesy : Stewart Calculus Early Transcendentals Sixth Edition *
The answer is 0.90689968211.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
We can ignore the circles that are tangent to the triangle(the outer layer of circles),then it is as same as a circle inscribed in a regular hexagon,so it's
2
3
π
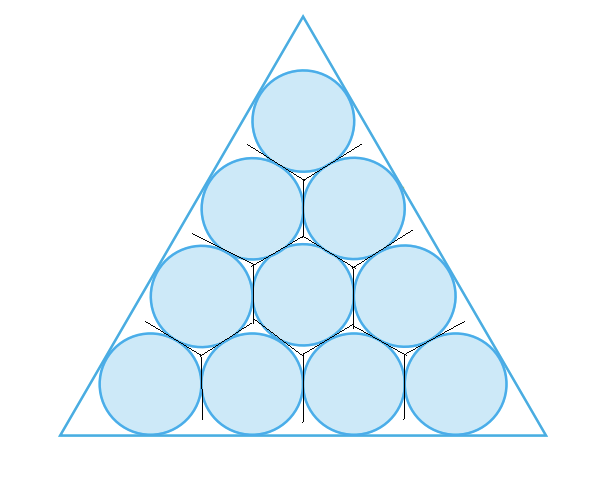 (We could cut the triangle in this way,and look at the circle in the middle.It's inscribed in a hexagon.)
(We could cut the triangle in this way,and look at the circle in the middle.It's inscribed in a hexagon.)
(Though we should ignore 9 circles when n = 4 ,but when n gets bigger,we can actually ignore it because the circles we ignore = 3 n − 3 ,but the total of the triangle = 2 n ( n + 1 ) )
Sounds interesting..... only I don't understand what you mean by that. Could you elaborate?
Log in to reply
I edited it.Maybe it'll help.
Let us call each circle has radius as R . The total ammount of circles T will be:
T = i = 1 ∑ n i = 2 n 2 + n
So:
B = T ⋅ π R 2
B = 2 π R 2 ( n 2 + n )
Let us call the triangle side as S . Looking at the base, the distance from the center of the leftmost circle to the center of the rightmost circle is 2 R ⋅ ( n − 1 ) . The part at the left of center of the leftmost circle or at the right ot the center of the rightmost circle is one cathetus of a right triangle, adjacent to a side which angle is 3 0 o and with other cathetus equal to R . So, this part is equal to R 3 and, since there are two of these parts:
S = 2 R ( n − 1 + 3 )
So:
A = 4 S 2 3
A = R 2 [ n 2 3 + ( 6 − 2 3 ) n + ( 4 3 − 6 ) ]
Thus:
L = n → ∞ lim A B
L = n → ∞ lim 2 R 2 [ n 2 3 + ( 6 − 2 3 ) n + ( 4 3 − 6 ) ] π R 2 ( n 2 + n )
L = 2 3 π ≈ 0 . 9 0 7
In limiting case n (2r) = l. So, r = l/(2n) . Area of all circles/Total area =(appx) (pi /8)/(root(3)/4) = pi/(2 root(3))
Chew-Seong Cheong's solution is close the expected solution I started off with!
Let the radius of the circle be r and the side length of the equivalent triangle containing n rows of circles be a . From the figure, we note that a = 2 r ( n − 1 ) + 2 3 r = 2 r ( n − 1 + 3 ) . Then the area of the triangle is A = 2 1 a × 2 3 a = 3 r 2 ( n − 1 + 3 ) 2 .
For n rows of circles, there are k = 1 ∑ n k = 2 n ( n + 1 ) circles. Therefore, the area of all the circles B = 2 n ( n + 1 ) π r 2 .
Now we have:
n → ∞ lim A B = n → ∞ lim 2 3 r 2 ( n − 1 + 3 ) 2 n ( n + 1 ) π r 2 = n → ∞ lim 2 3 ( 1 − n 1 − 3 ) 2 ( 1 + n 1 ) π = 2 3 ( 1 − n 1 − 3 0 ) 2 ( 1 + n 1 0 ) π = 2 3 π ≈ 0 . 9 0 7 Divide up and down by n 2