Calculate volume of a uniform tetradecahederon
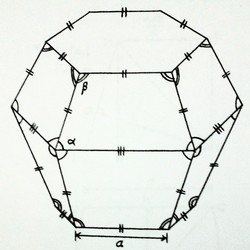 The diagram above shows a uniform tetradecahedron that has 2 congruent regular hexagonal faces each with side of length a=20 cm & 12 congruent trapezoidal faces each having three equal sides each a=20 cm. All its 18 vertices eventually & exactly lie on a spherical surface with a certain radius. Find out the volume (in cubic cm.) of the solid.
The diagram above shows a uniform tetradecahedron that has 2 congruent regular hexagonal faces each with side of length a=20 cm & 12 congruent trapezoidal faces each having three equal sides each a=20 cm. All its 18 vertices eventually & exactly lie on a spherical surface with a certain radius. Find out the volume (in cubic cm.) of the solid.
The answer is 54571.61458.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The solid is shown with all sides a = 20 in green and those on the 'equator' with length (R = circumscribing radius) in white. Take the central plane of symmetry yielding a hexagonal cross section shown.
R cos α = 2 0 and 2 R sin 2 α = 2 0 equating the two gives a quadratic in sin 2 α solving which gives sin 2 α = 2 3 − 1 that is α = 4 2 . 9 4 and R = 27.321
Area of top hexagon A T = 1 0 3 9 . 2 3 and area of equatorial hexagon A E = 1 9 3 9 . 2 3 Height of the two frustra of hexagonal pyramids = R sin α = 1 8 . 6 1 2
Volume of the solid = 2 x volume of each frustrum = 3 2 h ( A T + A T × A E + A E ) = 5 4 5 7 2
@Niranjan Khanderia