Calculating Armageddon
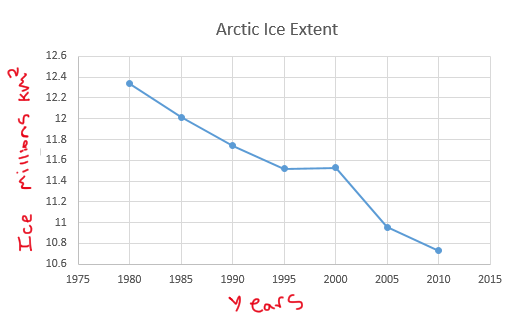Question: Within what year will the Arctic Ice Extent be equal to zero? Furthermore, what will the C02 level be in this year?
Use only the data provided below:
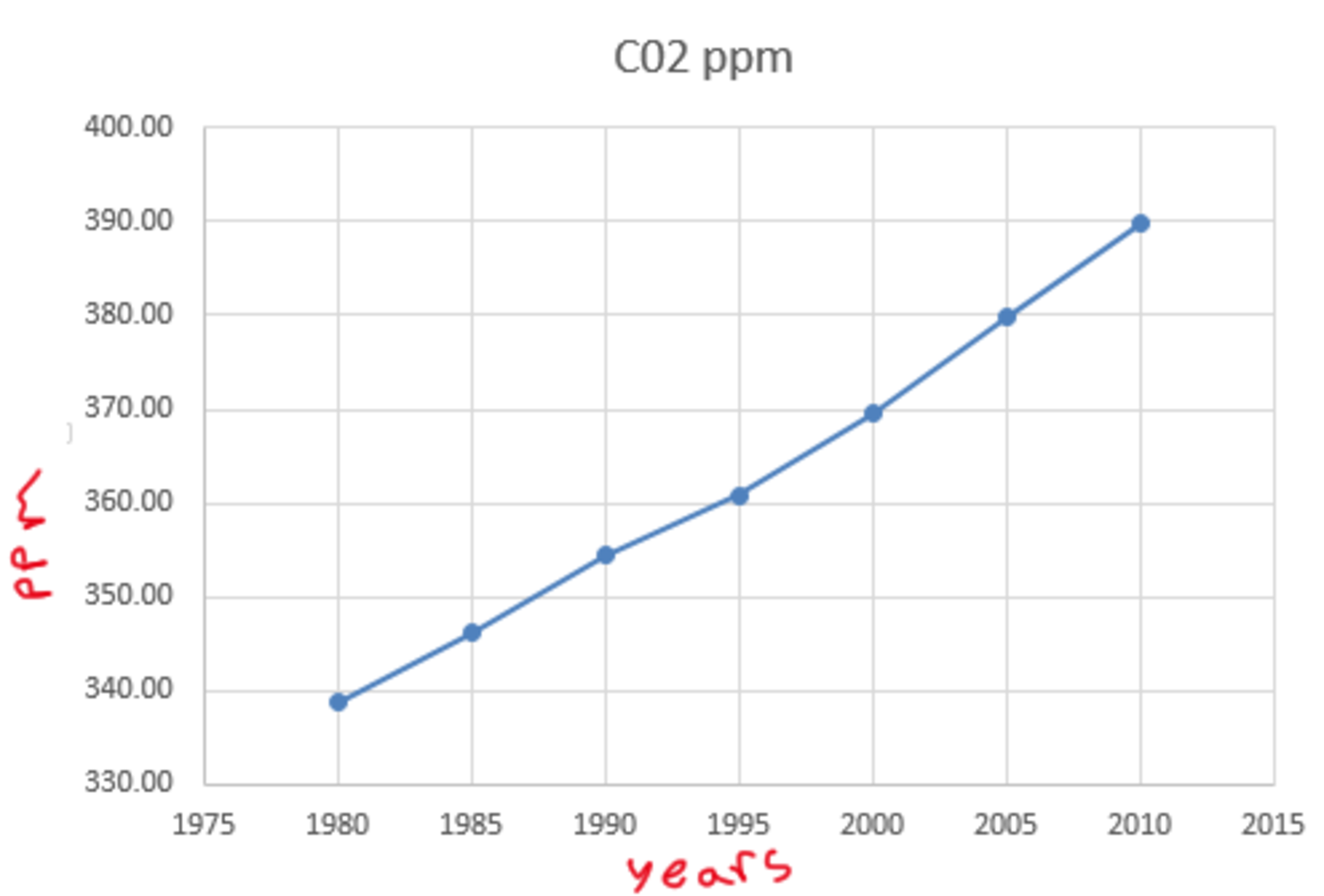
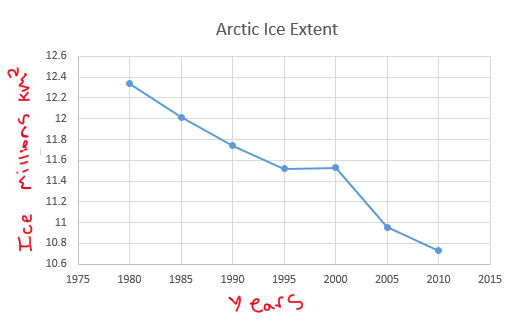
Footnote
The data in the images was derived from
National Snow and Ice Data Center
NOAA-ESRL Atmospheric C02 PPM Records
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
Thanks for sharing such a depressing fact :(
Is there any reason to believe that these trends are very linear? Considering that CO2 emissions increased by 15% in only 30 years, I'm inclined to think that it's exponential, if not quadratic.
This method can be solved by deriving the linear regression line. Therefore you will approach this problem with linear regression Analysis. Since the C02 level is increasing as the Years pass, we can perform our first linear regression analysis by treating Year as an independent variable and C02 ppm as a dependent variable. Thus we derive the first linear regression line:
year(1.69)-3002.84 = C02ppm
Next we analyze the correlation between C02ppm and Arctic Ice Extent. In this analysis we treat C02ppm as an independent variable and Arctic Ice Extent as a dependent variable. Thus deriving the second linear regression line:
C02ppm(-0.03)+22.56=Arctic Ice km^2
Now remember the question, we are finding the year in which the Arctic Ice Extent is zero. So we substitute Arctic Ice Extent with zero in our second linear regression line equation and solve for C02ppm:
C02ppm(-0.03)+22.56=0
C02ppm=752
Next we substitute C02ppm in our first regression line equation with 752 and solve for the year:
year(1.69)-3002.84 = 752
year = 2221.8