Calculations like this are why NBA players take so long to shoot free throws
An NBA basketball player want to score 3 points, so he shoots the ball right before the 3-point-line (which is d = 6 . 2 5 m horizontally away from the basket). The difference in height from where he releases the ball and the basket is roughly h = 1 m . Given the gravitational acceleration a g = − 9 . 8 m/s 2 , at what angle to the horizontal in degrees did he shoot the ball if the horizontal speed of the ball is 8 . 7 1 m/s ?
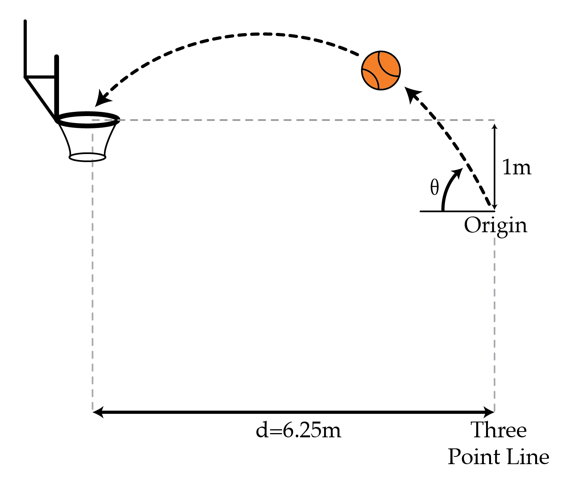
Details and assumptions
- You may neglect air resistance.
The answer is 29.41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
X distance = 6.25 m Y distance = 1 m X vel = 8.71 m/s T = 6.25 m / 8.71 m/s = .717566 seconds Ball drop = AT^2/2 = 9.8 x .717566^2/2 = 2.523 m Total height required = 2.523 + 1 = 3.523 m Angle = ARC TAN 3.523 / 6.25 = 29.409 degree
First of all, we note the difference between our horizontal and vertical components.Now we want to compute for the time which we will be using for computing the vertical component.
- d x = v x × t
- 6.25 m = 8.71 s m × t
- t= 8 . 7 1 s m 6 . 2 5 m
- t = 0.72 seconds
Solving for our v y :
-
d y = v y t + 2 g t 2
-
1 m = v y × 0 . 7 2 s + 2 ( − 9 . 8 s 2 m ) ( 0 . 7 2 s ) 2
- v y = 0 . 7 2 s 3 . 5 4 m
- v y = 4.91 s m
Solving for the our θ :
- arctan( 8 . 7 1 4 . 9 1 ) = θ
- θ = 2 9 . 4 1
( For simplicity I rounded off some variables but in my actual solution I put their exact values)
Why is D y = 1 m ? Shouldn't t = 0 , 7 2 s be for the whole trajectory the ball makes until it arrives to the net?
AS WE KNOW THE EQUATION OF TRAJECTORY FOR A PARABOLA IS y = xtan(A) - gx^2/2v^2cos^2(A).ALSO HORIZONTAL VELOCITY = vcos(A)=8.71. PUTTING x=6.25m AND y=1m 1 = 6.25tan(A) - 9.8(6.25)^2/2(vcosA)^2 or 1 = 6.25tan(A) - 4.9(6.25/8.71)^2 [ vcos(A)=8.71] or 1 = 6.25tan(A) - 2.523 or 3.523 = 6.25tan(A) or tan(A) = 3.523/6.25 or A = 29.049 degree. HENCE LAUNCH ANGLE IS 29.049 DEGREE.
X distance = 6.25 m
Y distance = 1 m
X velocity = 8.71 m/s
T = 6.25 m / 8.71 m/s = .717566 seconds
Ball drop = angle * 0.5T^2 = 9.8 * 0.5 * .717566^2 = 2.523 m
Total height required = 2.523 + 1 = 3.523 m
Angle = arctan (3.523 / 6.25) = 29.409 degrees
Let velocity of ball be 'v' m/s, angle be 'x' degrees, range be 'd' m.
Given, d=6.25m, vcos(x) = 8.71 m/s .....................(i)
So, vcos(x) * t = 6.25
t = 0.7175s
1 = vsin(x) * t - 0.5 * 9.8 * (0.7175) ^2 ...................(from second equation of motion)
vsin(x) = 4.906 m/s ......................(ii)
Squaring and adding (i) & (ii)
v = 9.996 m/s
From (i), we get cos(x) = (8.71/9.996)
cos(x) = 0.871
x = 29.42 degrees. (Ans)
X distance = 6.25 m
Y distance = 1 m
X vel = 8.71 m/s
T = 6.25 m / 8.71 m/s = .717566 seconds
Ball drop = AT^2/2 = 9.8 x .717566^2/2 = 2.523 m
Total height required = 2.523 + 1 = 3.523 m
Angle = ARC TAN 3.523 / 6.25 = 29.409 degrees
Let v be the velocity of the ball at launch, and v cos θ = v x be the horizontal velocity. Then we have
Δ x = v x t Δ y = ( v sin θ ) t + 2 1 g t 2
Solving for t in the first equation, we have t = v x Δ x . Now, note that v sin θ = v x tan θ . Substituting that expression, as well as the value obtained for t into the second equation, we have
Δ y = ( v x tan θ ) ( v x Δ x ) + 2 1 g ( v x Δ x ) 2
After simplifying and solving for θ (which is clearly in ( 0 , π / 2 ) , we have
θ = arctan [ ( Δ y − 2 1 g ( v x Δ x ) 2 ) / Δ x ]
Plugging in g = − 9 . 8 , v x = 8 . 7 1 , Δ x = 6 . 2 5 , Δ y = 1 , we get θ = 2 9 . 4 0 9 °
In projectile motion, the velocity of the object has two components: horizontal and vertical. These components are perpendicular to each other, so the key to finding the angle is to solve for the vertical component of velocity and then use right triangle trigonometry. Since you have the horizontal distance traveled and the horizontal velocity, you can solve for t with v x t = δ x , which gives t = 0.718 s. Because the time it takes for the ball to travel the horizontal distance (6.25 m) is equal to the time it takes for the ball to travel the vertical distance (1 m), you can plug this value for t into the equation for displacement in the vertical direction δ y = v y t − 2 1 g t 2 since the acceleration in this case is -g. Plugging in the values for δ y , t,and g, you have v y = 4 . 9 1 m/s. Now that you have v x and v y , the angle is tan − 1 = v x v y = 2 9 . 4 degrees.