Calculations of pressure under pressure!

Classical Mechanics Level 2

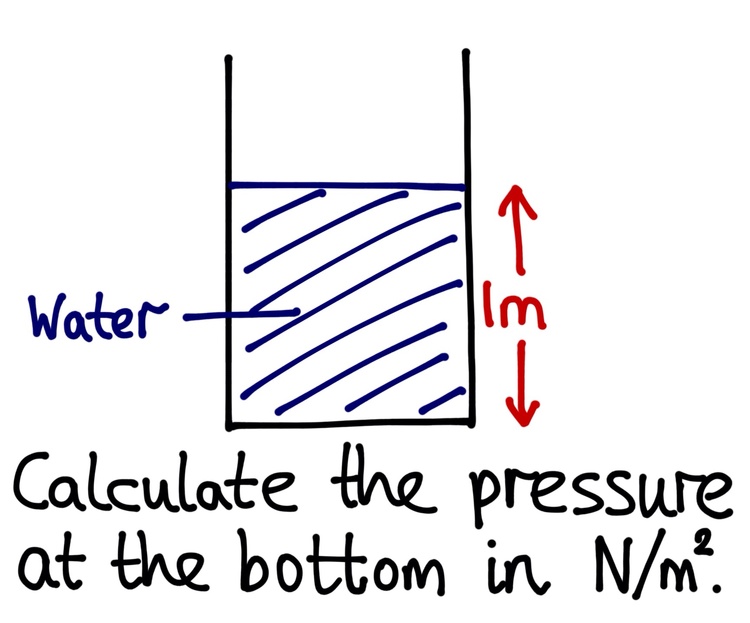Calculate the water pressure in $\mathrm{N/m^2}$ at the bottom of a pool $1\text{ m}$ deep, assuming that $g = 10 \text{ N/kg}$ . Ignore atmospheric pressure.

10 1 10000 1000

2 solutions

Discussions for this problem are now closed

Michael Ng
Dec 20, 2014

Pressure $= \rho gh = 1000 \times 10 \times 1 = \boxed{10000N/m^2}$ .

You are only calculating the pressure difference between the bottom and surface, if you want to calculate the actual pressure, you have to add the atmospheric pressure.

思澄馮 - 6 years, 5 months ago

Correct. But the one asked in the question is the pressure at the bottom of the tank and also it says Discount atmospheric pressure.

Aries Licup - 6 years, 5 months ago

That is a great point. Thank you.

Michael Ng - 6 years, 5 months ago

'p' signifies what

Anubhav Baranawal - 6 years, 5 months ago

$p$ is the density; in this case we have water so it equals $1000\mathrm{kg/m^3}$ .

Michael Ng - 6 years, 5 months ago

If you wanted to know more, density is represented by the Greek letter rho - \rho or \varrho . Rho is used for loads of things in science and maths, like Spearman's Rank Correlation Coefficient.

Mukul Rathi - 6 years, 5 months ago

Vishal S
Jan 10, 2015

Pressure = $\rho$ gh, where $\rho$ =density, g=acceleration due to gravity, h=height i.e.depth

By substituting the given values, we get

$1000 \times10 \times 1$ = $\boxed{10000 N/m^{2} }$

well done giving detail thanks

Gul Khan - 6 years, 5 months ago

Calculations of pressure under pressure!

2 solutions

Discussions for this problem are now closed

0 pending reports