Calculative or not...?

Geometry Level pending

A rectangular sheet of a paper(63cm x 42cm) is folded in two ways to make two cylinders. The first cylinder is made by folding the paper along its length and the second one is made by folding the paper along its breadth. Find the ratio of the volumes of the two cylinders.

2:5 1:3 5:3 3:2 4:7

Shubham Poddar by Shubham Poddar , 29, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

After revolving, it forms two regular cylinders.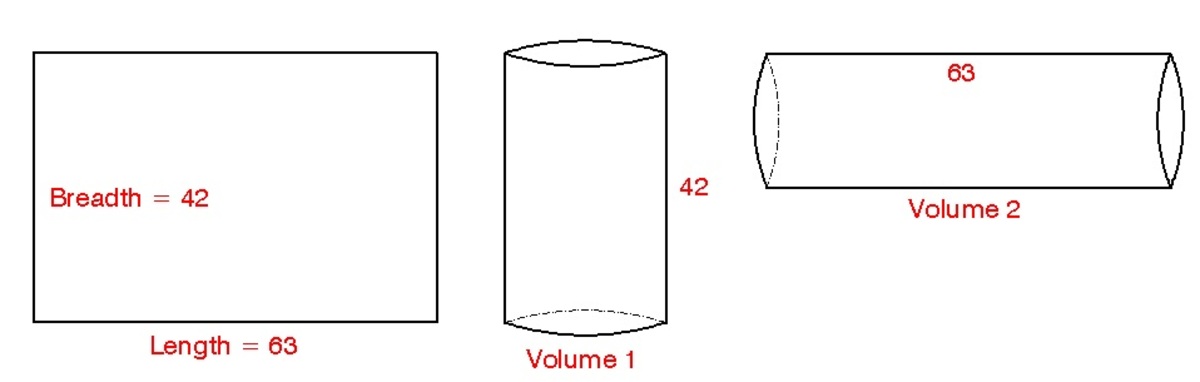

Solving for the volume of the first cylinder

The length of the rectangle is equal to the circumference of the base of the first cylinder.

c 1 = 2 π r 1 c_1 = 2\pi r_1

63 = 2 π r 1 63 = 2\pi r_1

r 1 = 63 2 π r_1 = \frac{63}{2\pi}

V 1 = π ( 63 2 π ) 2 ( 42 ) = 41674.5 π V_1 = \pi(\frac{63}{2\pi})^2(42) = \frac{41674.5}{\pi}

Solving for the volume of the second cylinder

The breadth of the rectangle is the circumference of the base of the cylinder**

c 2 = 2 π r 2 c_2 = 2\pi r_2

42 = 2 π r 2 42 = 2\pi r_2

r 2 = 21 π r_2 = \frac{21}{\pi}

V 2 = π ( 21 π ) 2 ( 63 ) = 27783 π V_2 = \pi(\frac{21}{\pi})^2(63) = \frac{27783}{\pi}

Solving for their ratios

V 1 V 2 = 27783 π 41674.5 π = 3 2 \frac{V_1}{V_2} = \frac{\frac{27783}{\pi}}{\frac{41674.5}{\pi}} = \frac{3}{2}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...