CALCULATORS ALLOWED....
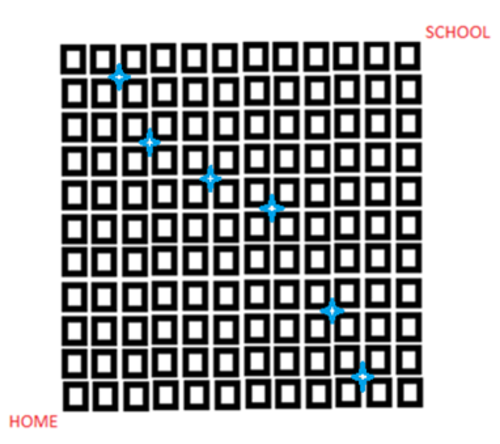Lucy woke up late in the morning... she quickly grasped her bag and left for school from her home... now she can reach her school in time only if she takes the shortest paths...
Moreover, there are some boulders in midst of some blocks (boulders have covered the whole path).... it means she strictly cannot cross those paths .... now how many shortest possible ways are there for Lucy which will lead her to school in time???
DIRECTIONS
- Consider the picture given above where the blue stars represents boulders....
- Lucy is at home or in other words at the corner of the first square...
- She should reach till the school or in other words till the end of right uppermost square.....
The answer is 584234.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Formula used:
If there is mXn rectangle divided into equal squares.. then the total no. of shortest ways is ((m+n)!)/(m!.n!) where m and n can also be equal….
We will start solving the question by dividing the given picture into different parts. In each part we will consider only one boulder.
Counting the number of possible ways is equal to no. of total ways – no. of non-possible ways.
CASE 1:
Let us consider just one boulder;
The no. of ways to go through that point is =12!/(10!.2!)×11!/(10!.1!)=726
CASE 2:
Let us consider the next boulder;
The no. of ways to go through that point is =11!/(8!.3!)×12!/(9!.3!)=36300
CASE 3:
Let us consider the third boulder;
The no. of ways to go through that point is =12!/(7!.5!)×11!/(4!.7!)=261360
CASE 4:
Let us consider the next boulder;
The no. of ways to go through that point is =13!/(6!.7!)×10!/(5!.5!)=432432
CASE 5:
Let us consider the next boulder;
The no. of ways to go through that point is =12!/(3!.9!)×11!/(3!.8!)=36300
CASE 6:
Now we will consider the last boulder;
The no. of ways to go through that point is =11!/(10!.1!)×12!/(10!.2!)=726
Thus all of these sums up to 767844.
Total no. of shortest ways to go through all these boxes without any restriction is
=23!/(11!.12!)=1352078
(since it is 11X12 rectangle...)
Therefore total no. of shortest ways in which Lucy can reach her school is 1352078-767844 = 5 8 4 2 3 4