Symmetry Spare Me This Awful Denominator
∫ − 1 1 1 + x 5 + 1 + x 1 0 d x = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
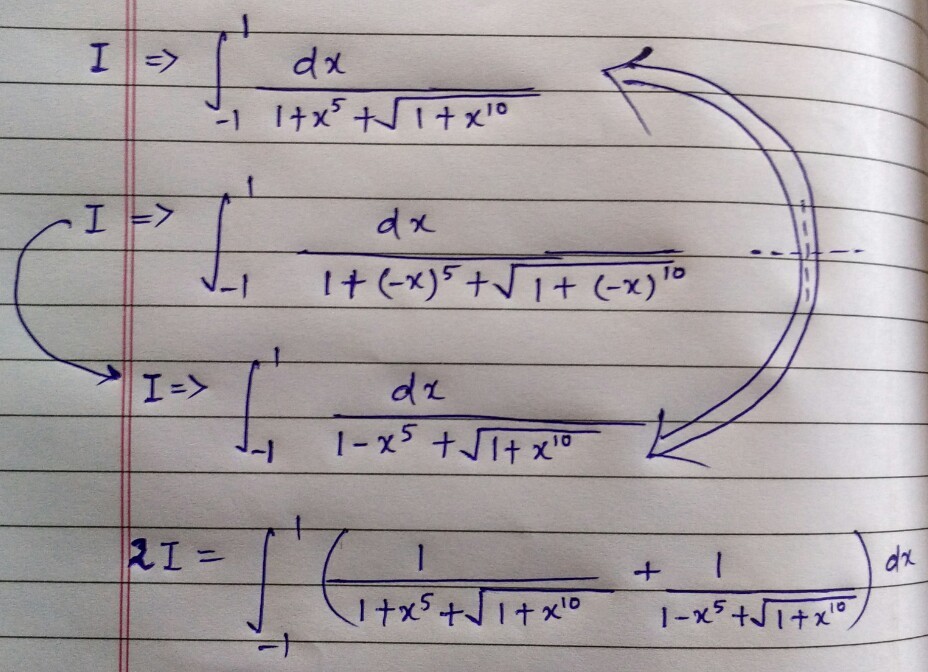
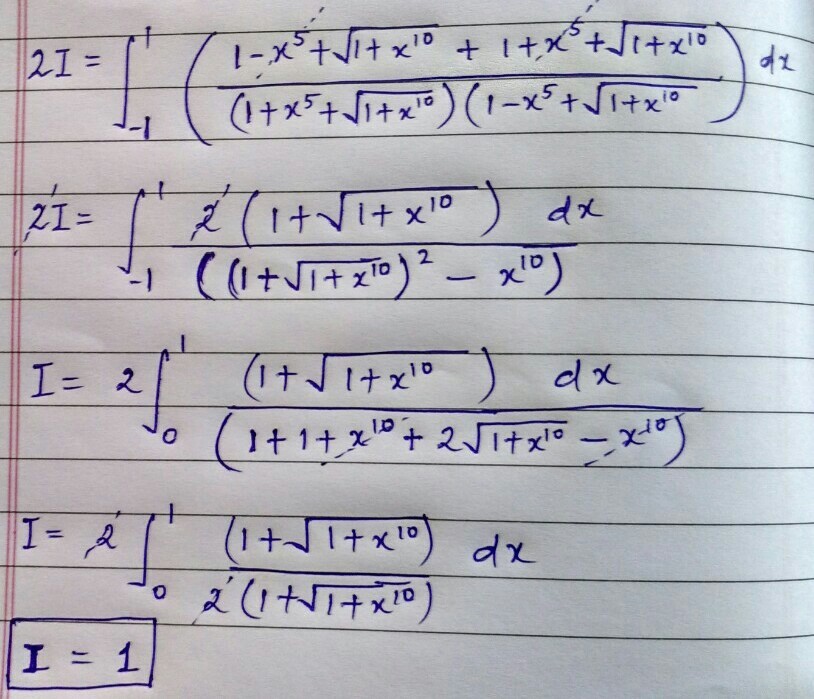
I don't understand why the integral from -1 to 1 is the same as twice the integral from 0 to 1 in the second to last step here.
Is it because without any x^5 terms the function is now even?
Log in to reply
I guess you don't need that step though, you would end up with the integral from -1 to 1 of dx/2, which still results in a 1. Nice problem!
Log in to reply
It's because its an even function (in that step) as all of the terms with x are x 1 0 .
How can you change your "x" for a "-x". I know it's a basic change of variables but wouldn't you need to state x = -z, change your dx for a dz, integrate from 1 to -1 and not from -1 to 1. I know it seems like it doesnt change much but a the 5th step, it would mean you can't do "(-x)^5 + (x)^5 = 0" because it would be "(-z)^5 + x^5" and this doesn't equal 0 at all. Can someone explain?
Log in to reply
What he is doing is flipping the x-axis around on the graph, and considering the new integral. Note that if you make the substitution x = -z, then yes you would integrate from 1 to -1, but you would also have a d z d x = − 1 which would cancel this switch out.
In addition:
∫ a b f ( x ) d x = ∫ a b f ( y ) d y