Tricky Calculus Question I

$\begin{aligned} I & = \int_\frac \pi 6^\frac \pi 3 \frac 1{1+\tan^{2018} x} dx & \small \color{#3D99F6} \text{Using }\int_a^b f(x) \ dx = \int_a^b f(a+b-x) \ dx \\ & = \frac 12 \int_\frac \pi 6^\frac \pi 3 \left(\frac 1{1+\tan^{2018} x} + \frac 1{1+\tan^{2018} \left(\frac \pi 2- x\right)} \right)dx \\ & = \frac 12 \int_\frac \pi 6^\frac \pi 3 \left(\frac 1{1+\tan^{2018} x} + \frac 1{1+\cot^{2018} x} \right)dx \\ & = \frac 12 \int_\frac \pi 6^\frac \pi 3 \left(\frac 1{1+\tan^{2018} x} + \frac 1{1+\frac 1{\tan^{2018} x}} \right)dx \\ & = \frac 12 \int_\frac \pi 6^\frac \pi 3 \left(\frac 1{1+\tan^{2018} x} + \frac {\tan^{2018}x}{\tan^{2018} x + 1} \right)dx \\ & = \frac 12 \int_\frac \pi 6^\frac \pi 3 dx = \frac x2 \ \bigg|_\frac \pi 6^\frac \pi 3 = \frac \pi{12} \end{aligned}$

Therefore, $k=\boxed{12}$ .

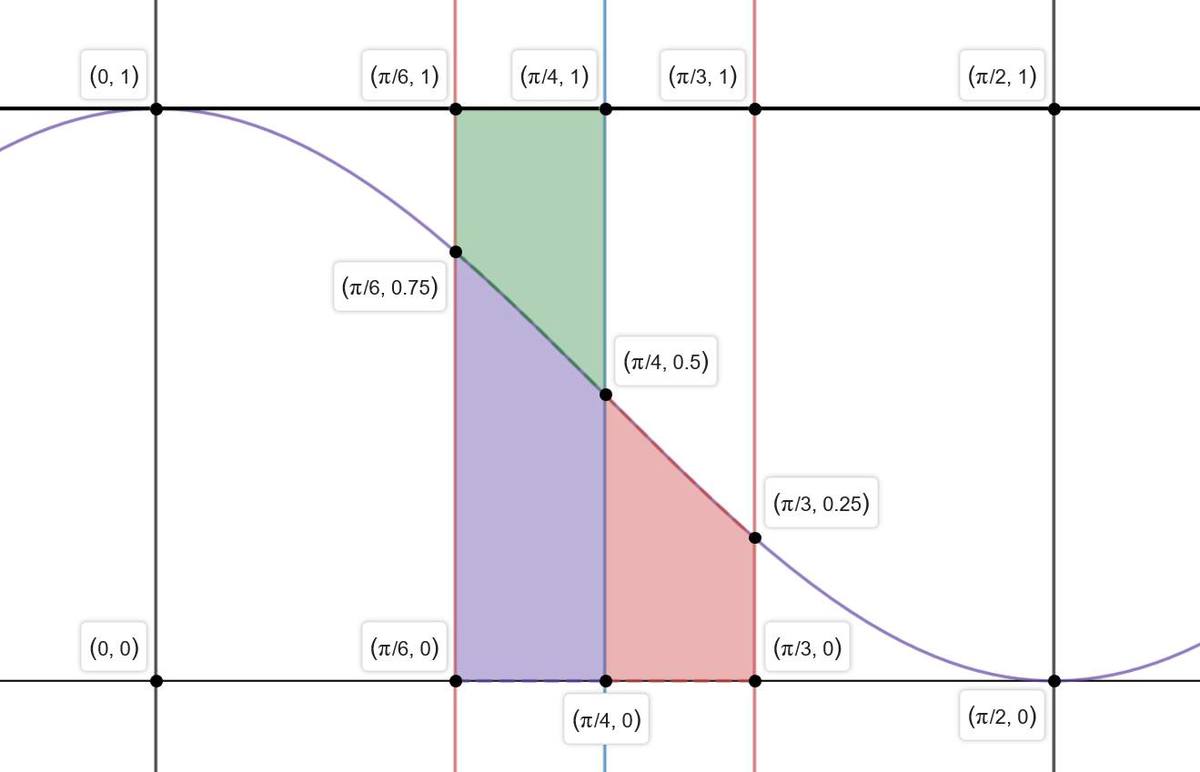
First, we need to prove that the graph of $f(x)$ is symmetry about a point between $0\leq x\leq \frac{\pi }{2}$ .

$0\leq x\leq \frac{\pi }{2}$ ,

$f\left ( \frac{\pi }{2}-x \right ) =\frac{1}{1+tan^{k}\left ( \frac{\pi }{2}-x \right )} =\frac{1}{1+cot^{k}(x)}$

$f(x)+f\left ( \frac{\pi }{2}-x \right ) =\frac{1}{1+tan^{k}(x)}+\frac{1}{1+cot^{k}(x)} =1$

$0\leq x\leq \frac{\pi }{4}$ ,

$f\left ( \frac{\pi }{4}-x \right ) = f\left ( \frac{\pi }{2}- \left ( \frac{\pi }{4} +x\right)\right) = 1-f\left ( \frac{\pi }{4} + x \right )$

$f\left ( \frac{\pi }{4}-x \right )+f\left ( \frac{\pi }{4} + x \right ) =1$

Thus, we found that the graph of $f(x)$ is symmetry about a point $\left ( \frac{\pi }{4}, \frac{1}{2}\right )$ between $0\leq x\leq \frac{\pi }{2}$ .

$\begin{aligned} \int_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{1}{1+tan^{k}(x)}dx &= \text{ Area of purple region}+ \text{ Area of red region} \\ &= \text{ Area of purple region}+ \text{ Area of green region} \text{ (based on symmetric)} \\ &= \left ( \frac{\pi }{4} - \frac{\pi }{3} \right )\cdot (1) \\ &= \frac{\pi}{12} \end{aligned}$

Substitute $k=2018$ ,

$\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{1}{1+tan^{2018}(x)}dx = \frac{\pi}{12}$