Calculus, Calculus Everywhere!

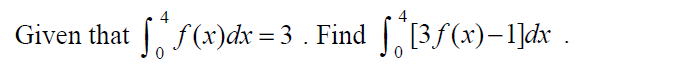
Disclaimer: DO NOT put this answer on your test. This is my thought precess and it works for this problem, but it may not represent the correct way to this question.

First, we are given that the integral of $f(x)$ in the interval [0,4] is 3. Therefore, 3 of these integrals will result in a 9. (In other words, the integral of $3f(x)$ in the interval [0,4] is 9.)

Now we are trying to figure out the integral of $3f(x)-1$ in the interval [0,4]. Think about it this way: if you have the graph $3f(x)$ in front of your eyes, and you want to translate it to $3f(x)-1$ . To do this, you would move the entire graph of $3f(x)$ one unit down. Now, the integral of $3f(x)-1$ is just like the integral of $3f(x)$ subtracted by a $1 \times 4$ $units^{2}$ rectangle.

Hence, our answer is $9-4= \boxed{5}$ .