Calculus, Geometry or Algebra?
x 2 − 6 x + 1 3 + x 2 + y 2 + y 2 − 8 y + 1 7
Given that x > 0 and y > 0 are real numbers, if the minimum of the above equation can be expressed as A B , where A and B are positive integers, and B is square free, input the product A B as your answer.
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Imagine the following diagram in which A B = 2 , B D = 3 , D F = 4 , and F G = 1 , and a path from A to G that passes through B D at C and D F at E :
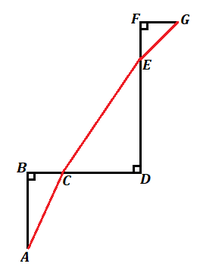
If x = C D and y = D E , then by the Pythagorean Theorem on the three right triangles, the length of the path is A C + C E + E G = 2 2 + ( 3 − x ) 2 + x 2 + y 2 + ( 4 − y ) 2 + 1 2 = x 2 − 6 x + 1 3 + x 2 + y 2 + y 2 − 8 y + 1 7 , the given equation.
This path is a minimum when it is a straight line:
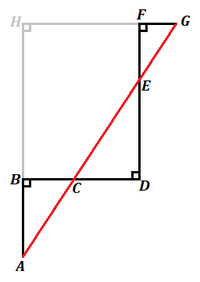
Since A H = A B + B H = A B + F D = 2 + 4 = 6 , and since H G = H F + F G = B D + F G = 3 + 1 = 4 , by Pythagorean Theorem on △ A H G the minimum path will be A G = A H 2 + H G 2 = 6 2 + 4 2 = 2 1 3 .
Therefore, A = 2 , B = 1 3 , and A B = 2 6 .
Both Sathvik Acharya and David Vreken have posted remarkable solutions. To accentuate how incredible their solutions are, I will post an atrocious solution.
Let f ( x , y ) denote the value of the expression that we want to minimize. Clearly f ( x , y ) has no maximum value because we can set either x or y to be unboundedly large. In other words, if f ( x , y ) has a critical point, it must be a minimum value.
At its critical points, both its partial derivatives must be 0, ∂ x ∂ f ( x , y ) = 0 ⇒ x 2 + y 2 x + x 2 − 6 x + 1 3 x − 3 = 0 ( 1 )
∂ y ∂ f ( x , y ) = 0 ⇒ x 2 + y 2 y + y 2 − 4 y + 1 7 y − 4 = 0 ( 2 )
From ( 1 ) , we can set y > 0 as the subject (I've omitted the tedious algebra):
y = x 2 − 6 x + 9 2 x ( 3 )
Likewise, from ( 2 ) , set x > 0 as the subject: x = ± y − 4 y ( 4 )
Substitute ( 4 ) into ( 3 ) yields ( x , y ) = ( 3 7 , 7 ) , ( 5 , 5 ) , ( 3 5 , 2 5 ) , ( 7 , 2 7 ) .
Trial and error shows that among these 4 critical points, ( x , y ) = ( 3 5 , 2 5 ) gives a smallest value of f ( x , y ) .
Hence, min ( f ( x , y ) ) = f ( 3 5 , 2 5 ) = 2 1 3 ⇒ A × B = 2 × 1 3 = 2 6 .
I am not gonna put a full explanation and it’s gonna use geometry and light ( physics )
The sum required is the sum of the distances in green
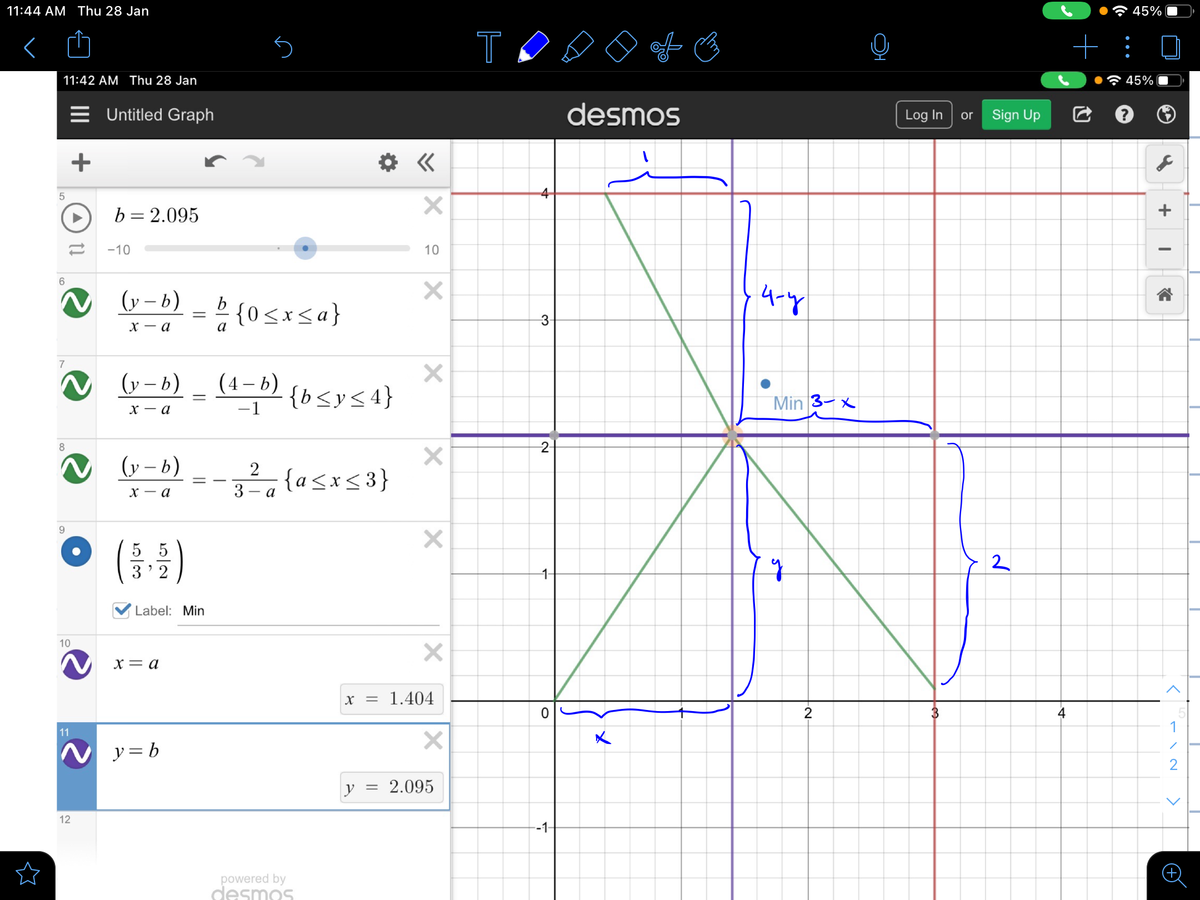
Here’s a Desmos link which is a little interactive on what the green distances are
If you notice it seems like there is a light ray coming from the origin bouncing off the point and landing on x=3 and y=4
If u keep the x coordinate constant and change the y coordinate you will also notice that point at which the light ray hits y=4 is constant
We can use fermats principle and see that when x=a acting as a mirror (purple vertical line) the first two distances ( from origin to point and point to y=4 ) can be minimised for a given x=a
Vice versa with y=b
The equations formed from these two will be that ( using similarity of triangles )
When x=a the sum of first two distances is minimised when y = a + 1 4 a
When y=b the sum of the next two distances (from origin to point, point to x=3) is minimised when x = b + 2 3 b
Solving these two equations with each other ( putting the value of x in a ) , we get x , y = 3 5 , 2 5
Putting these values in the equation given gives 2 1 3
@Michael Huang You can add physics to the title too now
Define vectors a 1 , a 2 , a 3 , a 4 as, a 1 a 2 a 3 a 4 = ( 3 − x ) i ^ + 2 j ^ = x i ^ + y j ^ = 1 i ^ + ( 4 − y ) j ^ = a 1 + a 2 + a 3 = ( 3 − x + x + 1 ) i ^ + ( 2 + y + 4 − y ) j ^ = 4 i ^ + 6 j ^ ⟹ ∣ a 1 ∣ = x 2 − 6 x + 1 3 ⟹ ∣ a 2 ∣ = x 2 + y 2 ⟹ ∣ a 3 ∣ = y 2 − 8 y + 1 7 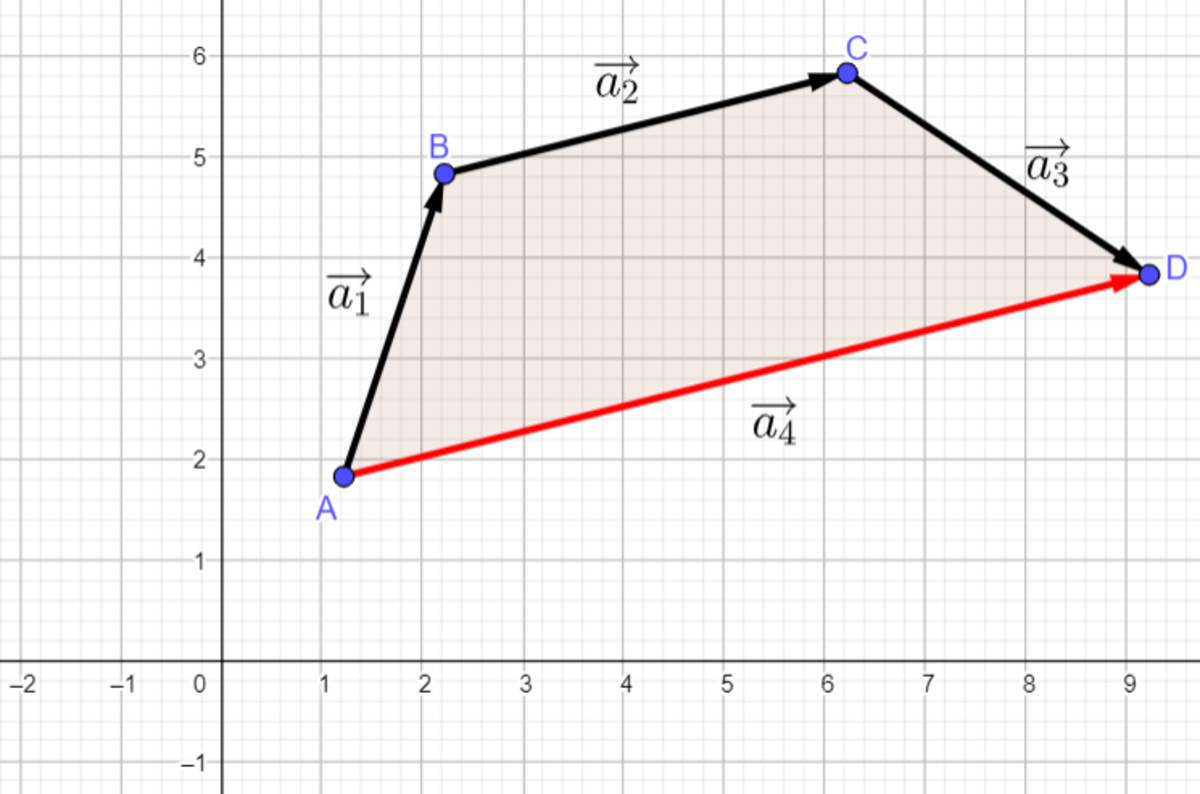 In a general quadrilateral,
the sum of the lengths of any three sides is greater than the length of the fourth side
, so we have,
∣
a
1
∣
+
∣
a
2
∣
+
∣
a
3
∣
≥
∣
a
4
∣
⟹
x
2
−
6
x
+
1
3
+
x
2
+
y
2
+
y
2
−
8
y
+
1
7
≥
4
2
+
6
2
=
5
2
Therefore, the four vectors must lie on a straight line for equality to be achieved and the minimum value of the expression is
5
2
=
2
1
3
⟹
A
B
=
2
6
In a general quadrilateral,
the sum of the lengths of any three sides is greater than the length of the fourth side
, so we have,
∣
a
1
∣
+
∣
a
2
∣
+
∣
a
3
∣
≥
∣
a
4
∣
⟹
x
2
−
6
x
+
1
3
+
x
2
+
y
2
+
y
2
−
8
y
+
1
7
≥
4
2
+
6
2
=
5
2
Therefore, the four vectors must lie on a straight line for equality to be achieved and the minimum value of the expression is
5
2
=
2
1
3
⟹
A
B
=
2
6