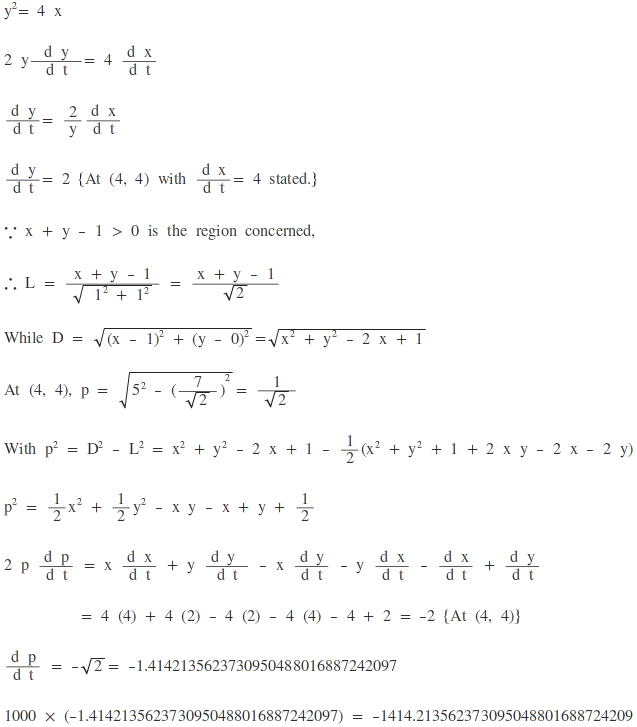Calculus In Parabola
Let S be the focus of y 2 = 4 x . Point P is moving on this curve such that its abscissa is increasing at a rate of 4 units per second. Then the rate of increase of the length of projection of S P on x + y = 1 when P is at ( 4 , 4 ) is γ .
Find 1 0 3 γ to 1 decimal place.
The answer is -1414.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
T
h
e
l
i
n
e
x
+
y
=
1
p
a
s
s
e
s
t
h
r
o
u
g
h
B
=
(
0
,
1
)
a
n
d
A
=
(
1
,
0
)
L
e
t
t
h
e
v
e
c
t
o
r
u
b
e
t
h
e
v
e
c
t
o
r
a
l
o
n
g
t
h
a
t
l
i
n
e
(
B
A
)
.
u
=
A
−
B
=
⟨
0
−
1
,
1
−
0
⟩
u
=
⟨
−
1
,
1
⟩
=
−
i
^
+
j
^
U
n
i
t
v
e
c
t
o
r
a
l
o
n
g
u
i
s
u
^
=
∣
u
∣
u
u
^
=
⟨
2
−
1
,
2
1
⟩
=
2
1
(
−
i
^
+
j
^
)
U
s
i
n
g
t
h
e
e
q
u
a
t
i
o
n
y
2
=
4
x
,
w
e
g
e
t
t
h
e
f
o
c
u
s
t
o
b
e
(
1
,
0
)
a
n
d
t
h
e
d
i
r
e
c
t
r
i
x
t
o
b
e
x
=
−
1
.
D
i
s
a
n
y
p
o
i
n
t
o
n
t
h
e
p
a
r
a
b
o
l
a
w
i
t
h
c
o
o
r
d
i
n
a
t
e
s
(
x
,
y
)
L
e
t
v
b
e
t
h
e
v
e
c
t
o
r
a
l
o
n
g
B
D
v
=
D
−
B
v
=
⟨
x
−
1
,
y
⟩
=
(
x
−
1
)
i
^
+
y
j
^
T
h
e
l
e
n
g
t
h
o
f
t
h
e
p
r
o
j
e
c
t
i
o
n
o
f
D
B
a
l
o
n
g
l
i
n
e
y
+
x
=
1
i
s
g
i
v
e
n
b
y
L
=
v
.
u
^
=
(
x
−
1
)
×
(
2
−
1
)
+
(
y
)
×
(
2
1
)
L
=
2
1
(
1
−
x
+
y
)
U
s
i
n
g
t
h
e
p
a
r
a
b
o
l
a
e
q
u
a
t
i
o
n
L
=
2
1
(
1
−
x
+
4
x
)
D
i
f
f
e
r
e
n
t
i
a
t
i
n
g
i
t
w
i
t
h
r
e
s
p
e
c
t
t
o
s
o
m
e
v
a
r
i
a
b
l
e
t
d
t
d
L
=
2
1
(
−
d
t
d
x
+
2
x
2
d
t
d
x
)
A
t
p
o
i
n
t
(
4
,
4
)
d
t
d
L
=
2
1
(
−
d
t
d
x
+
4
1
d
t
d
x
)
d
t
d
L
=
2
2
−
1
d
t
d
x
G
i
v
e
n
d
t
d
x
=
4
d
t
d
L
=
−
2
1
0
3
×
(
−
2
)
=
−
1
4
1
4
.
2
kindly provide image for second solution asap.