Calculus isn't Just Useful for Physics
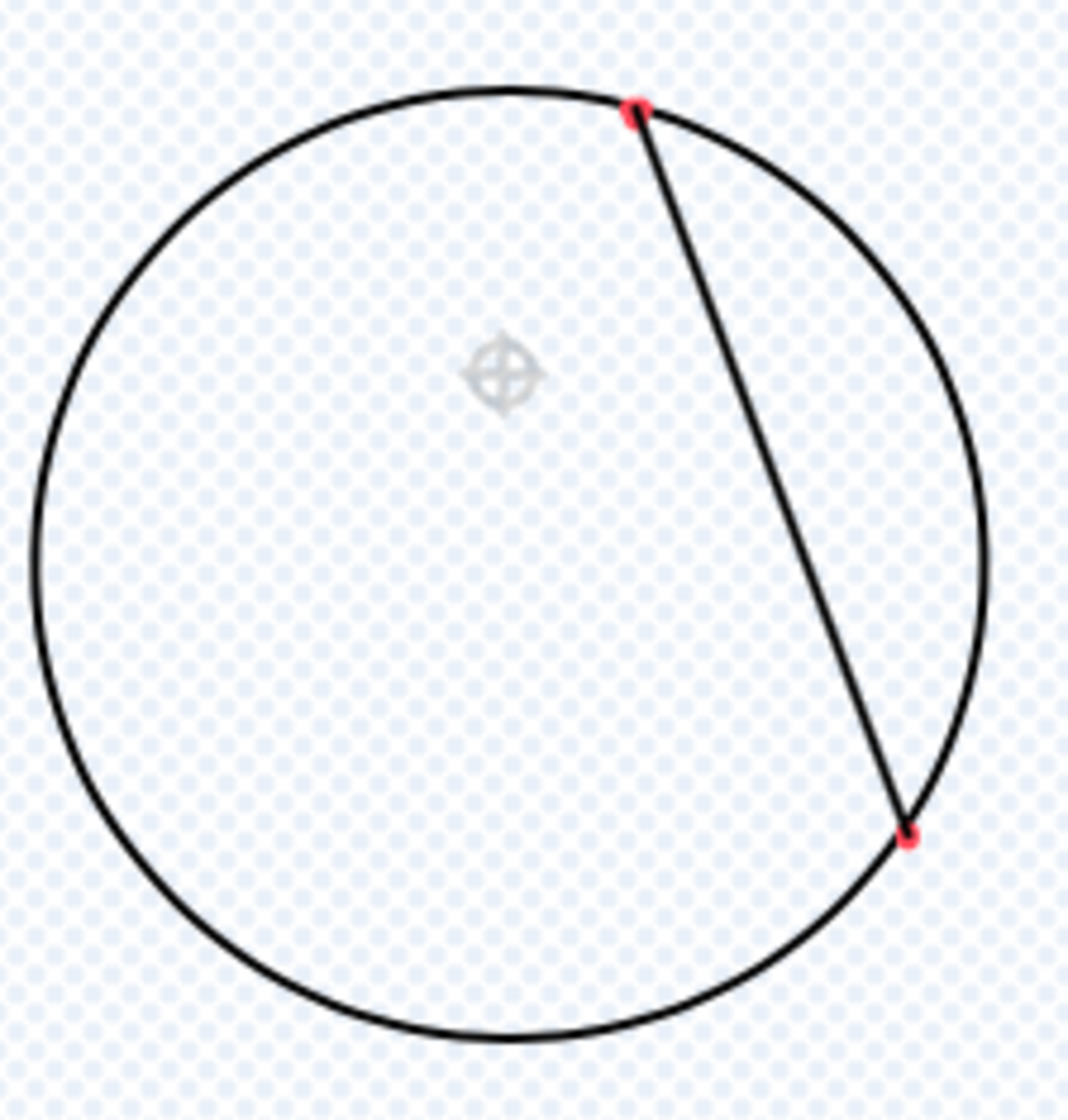 If 2 points are chosen randomly on the circumference of a circle of radius 1, what is the expected straight distance between the points?
If 2 points are chosen randomly on the circumference of a circle of radius 1, what is the expected straight distance between the points?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The first thing to realize is that we can set the first point to be anywhere we want, because regardless of where it is actually chosen, we can rotate the circle so that the first point is where we wanted it. Given this, we can set the first point to be on the bottom of the circle.
The second thing to realize is that we only need to consider the second point landing on one half of the circle because a circle is symmetrical.
For the second point, we can pick a number of points that are equally spaced on the semicircle and calculate the expected distance from the first point if we pick one of those points at random. To get the answer for the original problem, we need to calculate the average distance as the number of possible points to pick for the second point approaches infinity.
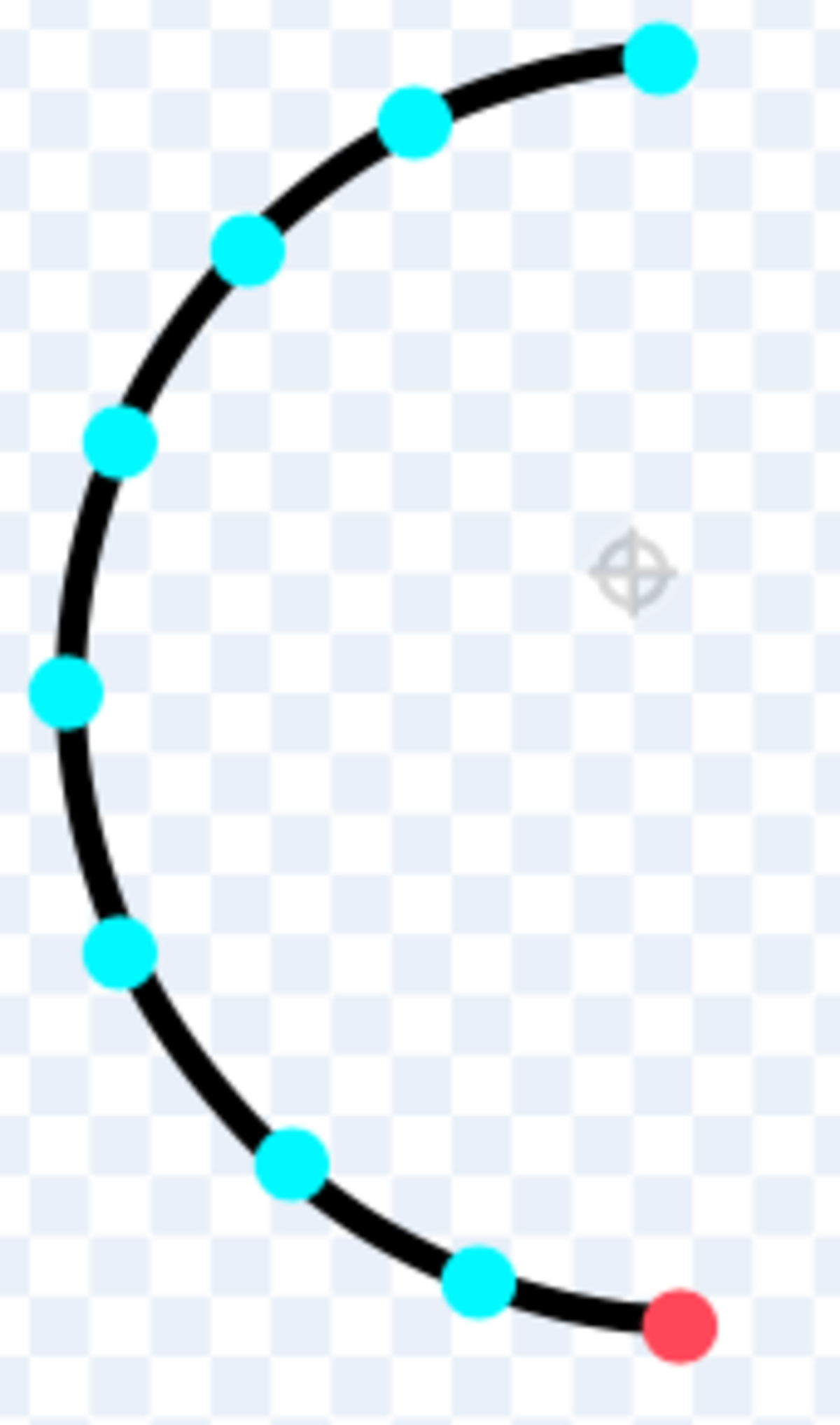
We can determine the distance from the first point to any of the possible second points by using the Law of Cosines: c = a 2 + b 2 − 2 a b c o s C
We know the radius is 1 and that all the arcs between the points are equal since we specified they were equally spaced. The total arc of the semicircle is π .
With all the information, we can determine the answer to our original problem is:
n → ∞ lim n 1 ( 2 − 2 c o s ( n π ) + 2 − 2 c o s ( n 2 π ) . . . 2 − 2 c o s ( n n π ) )
The Riemann sum states that ∫ 0 1 f ( x ) d x = n → ∞ lim n 1 ( f ( n 1 ) + f ( n 2 ) . . . f ( n n ) )
Every term inside the parentheses of the Riemann sum must be equal to the corresponding term in the parentheses of our answer.
So, f ( n 1 ) = 2 − 2 c o s ( π × n 1 )
f ( x ) = 2 − 2 c o s ( π x )
We need to find the integral from 0 to 1 of f ( x ) .
2 ∫ 1 − c o s ( π x ) d x
u = π x
π d u = d x
π 2 ∫ 1 − c o s u d u
π 2 ∫ s i n 2 u d u
v = 2 u
2 d v = d u
π 4 ∫ s i n v d v
π 4 ( − c o s v )
π 4 ( − c o s ( 2 u ) )
− π 4 c o s ( 2 π x )
Now, evaluating from 0 to 1:
0 − ( − π 4 )
π 4
Let us fix the position of one of the points and choose the other point randomly. Let the angle between the tangent to the circle at the fixed point and the line joining the two points be α . Then the required expected distance between the two points is
< l > = π 1 ∫ 0 π l d α = π 2 ∫ 0 2 π sin α d α = π 4 .