Calculus - Minimizing Distance
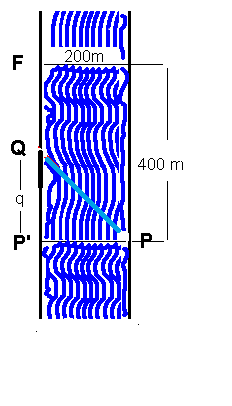 A power house, P, is on one bank of a straight river 200 m wide,
and a factory, F, is on the opposite bank 400m downstream from P.
The cable has to be taken across the river,
under water at a cost of $6/m.
On land the cost is $3/m. Tell the least cost with shortest angle?
A power house, P, is on one bank of a straight river 200 m wide,
and a factory, F, is on the opposite bank 400m downstream from P.
The cable has to be taken across the river,
under water at a cost of $6/m.
On land the cost is $3/m. Tell the least cost with shortest angle?
NOTE: path should be chosen so that the cost is minimized
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It can be seen that cost y is a function of distance q (as denoted in the diagram).
y = 4 0 0 − q + q 2 + 2 0 0 2
We can find the minimum of y by taking its derivative and equating with zero:
d q d y = − 1 + q 2 + 2 0 0 2 2 q = 0 .
Hence, q = 3 2 0 0 3 . The value of q obtained is a minimum as as can be seen by the second derivative test.
Let θ be the angle from the power house. tan θ = 6 0 0 2 0 0 3 = 3 3 . Thus, θ = π / 6 .