Calculus problem #63971
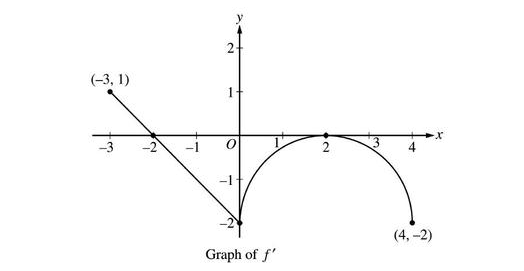
Suppose is a function defined on the closed interval with such that the graph of the derivative of on the interval is as shown in the above diagram. Find the -coordinates of the points of inflection of
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
for point of inflection f ′ ( x ) =0
The point at which the 2nd derivative switches sign is called the Inflation point. => The point x = 0 is also an inflation point. The slop of f' changes from -ve to +ve. similarly goes for x == 2.
We cannot find 2nd derivative of f at x == 0 because the LHL and RHL are not the same.