A calculus problem by Refaat M. Sayed
I = 0 ∫ ∞ 1 + 3 x + x 2 x d x = sin ( A ∘ ) sin ( 3 A ∘ ) π sin ( 2 A ∘ )
The equation above holds true for some positive integer A . Find the smallest possible value of A .
Clarification: Angles are measured in degrees.
This problem is part of the set of complex analysis problems .
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
By the way, nice problem, Mr @Refaat M. Sayed !
Please put π in the last two lines of the integral's solution to make it perfect
Relevant wiki: Cauchy Integral Formula
Consider the complex form of I = ∫ 0 ∞ f ( x ) d x = ∫ 0 ∞ x 2 + 3 x + 1 x d x ,
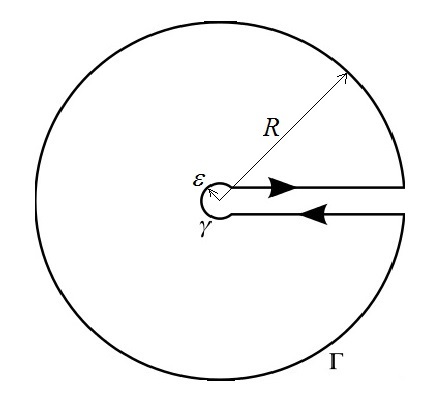
J = ∫ C z 2 + 3 z + 1 z d z = ∫ ϵ R f ( z ) d z + ∫ Γ f ( z ) d z + ∫ R ϵ f ( z ) d z + ∫ γ f ( z ) d z = ∫ ϵ R z 2 + 3 z + 1 z d z + ∫ R ϵ z 2 + 3 z + 1 z d z = 2 ∫ 0 ∞ x 2 + 3 x + 1 x d z As z has a branch cut, we use the keyhole contour. Note: R → ∞ lim ∫ Γ f ( z ) d z = 0 , ϵ → 0 lim ∫ γ f ( z ) d z = 0 See note: ∫ R ϵ f ( z ) d z = ∫ ϵ R f ( z ) d z
⟹ J = 2 I and then we have:
I = 2 1 ∫ C z 2 + 3 z + 1 z d z = 2 1 ∫ C ( z + 2 3 − 2 i ) ( z + 2 3 + 2 i ) z d z = 2 1 ∫ C ( z − e 6 5 π i ) ( z − e 6 7 π i ) z d z = 2 i 1 ∫ C ( z − e 6 5 π i z + z − e 6 7 π i z ) d z = 2 i 2 π i ( e 1 2 5 π i − e 1 2 7 π i ) = π ( cos 1 2 5 π + i sin 1 2 5 π − cos 1 2 7 π − i sin 1 2 7 π ) = π ( cos 1 2 5 π + i sin 1 2 5 π + cos 1 2 5 π − i sin 1 2 5 π ) = 2 π cos 1 2 5 π = 2 π sin 1 2 π = 2 π sin 1 5 ∘ = 2 1 × 1 π sin 1 5 ∘ = sin 3 0 ∘ sin 9 0 ∘ π sin 1 5 ∘ Two poles within the contour z = e 6 5 π i , e 6 7 π i By Cauchy integral formula
⟹ A = 3 0
Note:
J 1 = ∫ R ϵ z 2 + 3 z + 1 z d z = ∫ R ϵ z 2 + 3 z + 1 e 2 1 ln z d z = ∫ R ϵ z 2 + 3 z + 1 e 2 1 ( ln ∣ z ∣ + i ar g z ) d z = ∫ R ϵ z 2 + 3 z + 1 e 2 1 ln ∣ z ∣ e π i d z = ∫ R ϵ z 2 + 3 z + 1 − e 2 1 ln ∣ z ∣ d z = ∫ R ϵ z 2 + 3 z + 1 − z d z = ∫ ϵ R z 2 + 3 z + 1 z d z Note: ar g z = 2 π one revolution
I = ∫ 0 ∞ x 2 + 3 x + 1 x d x
Make x = u Then 2 x 1 d x = d u or d x = 2 u d u
I = 2 ∫ 0 ∞ u 4 + 3 u 2 + 1 u 2 d u
I = 2 ∫ 0 ∞ ( u 2 + 2 3 + j ) ⋅ ( u 2 + 2 3 − j ) u 2 d u
Being j the imaginary unit.
I = 2 ∫ 0 ∞ u 2 ( u 2 + e j π / 6 j − u 2 + e − j π / 6 j ) d u
I = 2 j ∫ 0 ∞ ( u 2 + e j π / 6 u 2 − u 2 + e − j π / 6 u 2 ) d u
I = 2 j [ ( u − e j π / 1 2 ⋅ a t a n ( u ⋅ e − j π / 1 2 ) ) ∣ ∣ ∣ 0 ∞ − ( u − e − j π / 1 2 ⋅ a t a n ( u ⋅ e j π / 1 2 ) ) ∣ ∣ ∣ 0 ∞ ]
I = 2 j ⋅ ( e − j π / 1 2 ⋅ 2 π − e j π / 1 2 ⋅ 2 π )
I = 2 π s i n ( 1 2 π )
I = 2 1 ⋅ 1 π s i n ( 1 2 π )
I = sin ( π / 6 ) ⋅ s i n ( 3 ⋅ π / 6 ) π s i n ( 2 π / 6 )
Hence A = π / 6 or, in degrees, A = 3 0 o
The powers of 3 0 divided by 7 generate a remainder in the pattern { 2 , 4 , 1 , 2 , 4 , 1 . . . } , i.e., 2 if the power is a multiple of 3 plus 1 , 4 if the power is a multiple of 3 plus 2 and 1 if the power is a multiple of 3 .
Since 3 0 is a multiple of 3 , the remainder is 1