Calisson
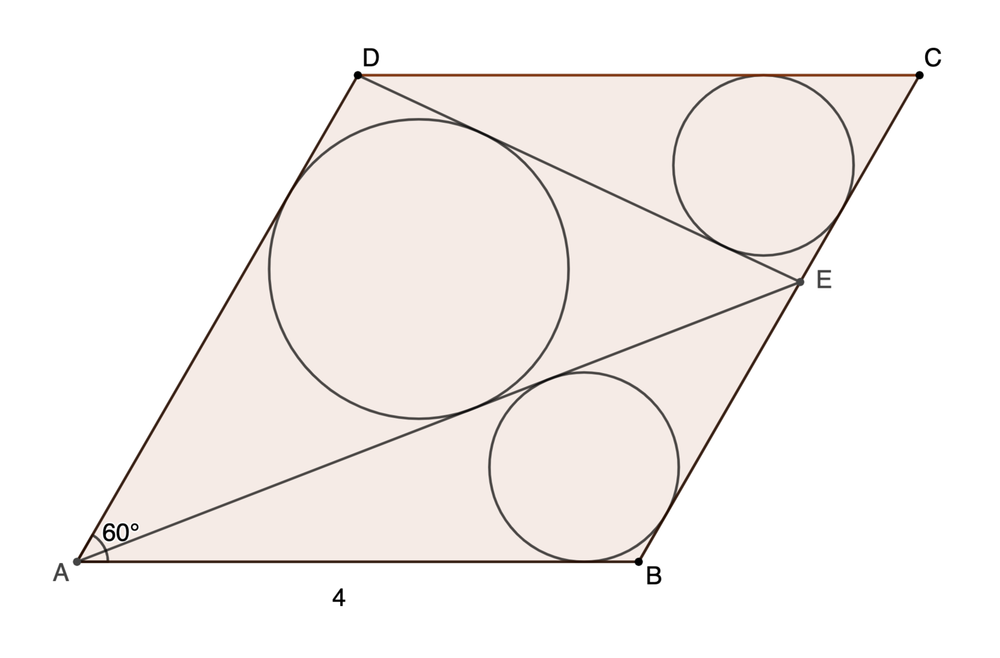
is a rhombus with an interior angle of and has side length . If the two small circles are congruent, what is the ratio of the radius of the large circle to the radius of a small circle? If this ratio is expressed as , where , , and are positive integers and is square-free, submit .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radius of the small circle be r and the radius of the large circle be R . For any triangle, the line joining a vertex and the incenter bisects the angle of the vertex. Consider △ A B E and its side A B ,
r cot 2 ∠ E A B + r cot 2 ∠ E B A r cot 2 θ + r cot 6 0 ∘ t r + 3 r ⟹ t = A B = 4 = 4 = 4 − 3 r r Let ∠ E A B = θ and t = tan 2 θ
Let ∠ C D E = ϕ and u = tan 2 ϕ . Similarly for △ C D E and side C D , u r + 3 r = 4 ⟹ u = 4 − 3 r r .
Now consider B E + E C = B C :
r cot 6 0 ∘ + r cot 2 6 0 ∘ − θ + r cot 2 1 2 0 ∘ − ϕ + r cot 3 0 ∘ 3 r + 1 − 3 t 3 + t r + 3 − u 1 + 3 u r + 3 r 3 r + 3 − r 3 r + 3 − r r + 3 r 3 4 r + 3 − r 4 r 3 r + 3 − r r r 2 − 3 3 r + 3 ( 3 − r ) 2 − 3 r ( r 3 − 1 ) 2 − ( r 3 − 1 ) − 1 ⟹ r 3 − 1 = 4 = 4 = 4 = 4 = 1 = 0 = 0 = 0 = φ Divide both sides by r 2 where φ = 2 1 + 5 denotes the golden ratio.
Now consider △ A D E and side D A .
R cot 2 6 0 ∘ − θ + R cot 2 1 2 0 ∘ − ϕ R ( 1 − 3 t 3 + t + 3 − u 1 + 3 u ) r R ( 1 − 3 t 3 + t r + 3 − u 1 + 3 u r ) r R ( 3 − r 4 r ) ⟹ r R = 4 = 4 = 4 = 4 = r 3 − 1 = φ = 2 1 + 5 See above
Therefore a + b + c = 1 + 5 + 3 = 8 .