Can I retrace the altitude?
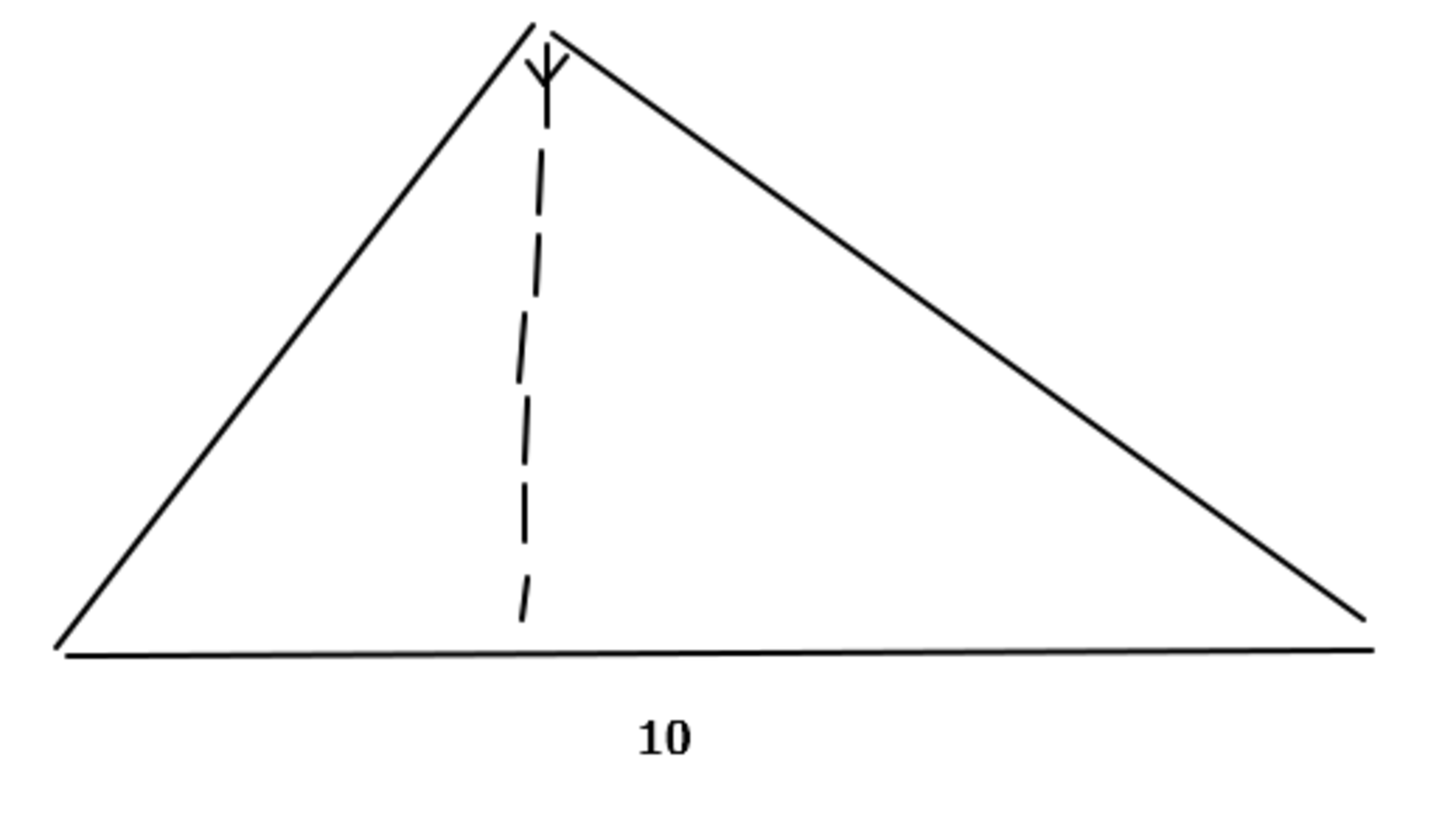
As shown above, I've drawn a right triangle with a hypotenuse of 10. However, I could not figure out the altitude (as shown in the dotted lines).
Which of the following could be the altitude in question?
Select one or more
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The locus of right angles of all possible right triangles with a given hypotenuse is a semicircle with the same diameter, since the angle inscribed in a semicircle is always a right angle. Therefore, the different altitudes of a right triangle with a hypotenuse of 1 0 will correspond with the different heights of the semicircle with a diameter of 1 0 , which would be 0 < x ≤ 5 .
This means that out of the options given, 3 , 4 , and 5 are possible altitudes, but not 6 .