Chain of Pearls

Here is how to do it the easy way;

• When we had only one pearl, there was only one form. Now, when we have another pearl added to it, we can place it to 3 different positions as follows;

1. Parallel to A---B (as A---B---C)

2. Above B in A---B

3. Below B in A---B (this form would be simply a reflection of above second form therefore we neglect it)

Therefore there are only two unique forms of the chain formed with $3$ pearls.

• After you know the two different forms above, you can extend them one by one by adding one more pearl to its all possible positions.

Following are all the possible forms or shapes when we have five pearls;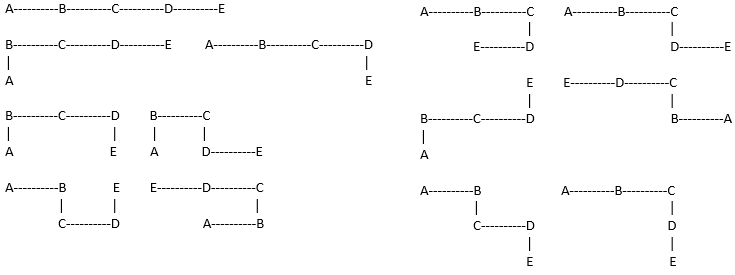

As we see here, there are $13$ unique structures or forms of the chain formed with $5$ pearls.

This problem can be solved by systematically enumerating all possible chains while eliminating those which are equivalent due to rotation or reflection symmetries. For this purpose, let us encode the orientation of each pearl in a chain with one of the following symbols describing the path from the current pearl to its consecutive one:

S – go straight

R - turn right

L – turn left

A chain of $N$ pearls can be represented by a string of $N-2$ symbols (the first and last pearls need not be included) for a total of $3^{N-2}$ possible strings. For the case of 5 peals, this gives a total of 27 possibilities. This number includes also all possible symmetries which need to be excluded.

As an example, the string RLL represents this chain: It is easy to see that strings RXX are equivalent to strings LXX (where X stands for any symbol) due to reflection. We can therefore ignore LXX strings, leaving only 18 possibilities as follows:

Chains #3,7,8,9 are equivalent to other chains and therefore are excluded from the counting.

Chain #14 is possible if you allow the pearls to occupy the same position (for example, lie on top of each other).

Therefore, the number of unique chains is either 14 or 13 (if chain #14 is not allowed).