Can It Be Traced?
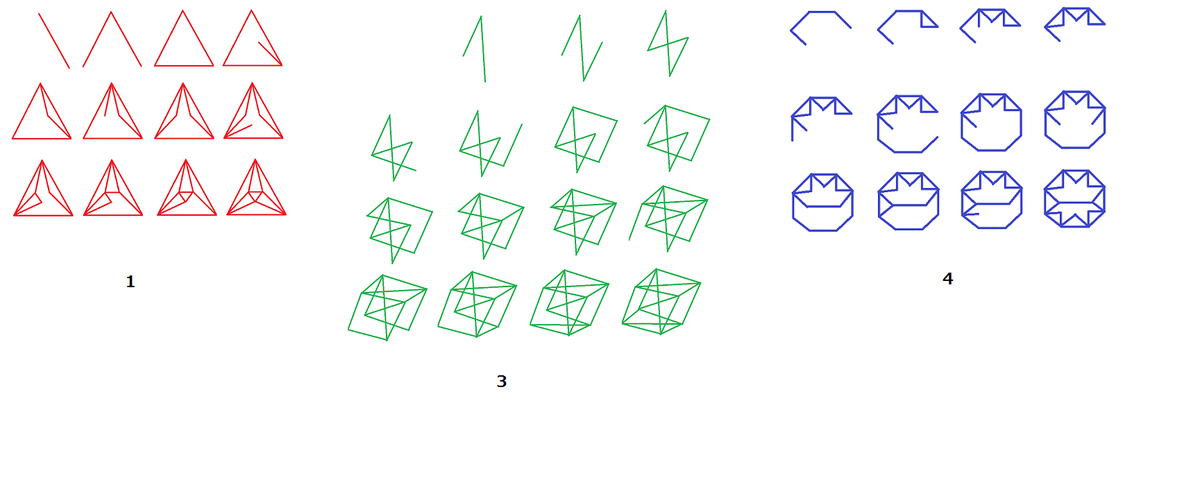
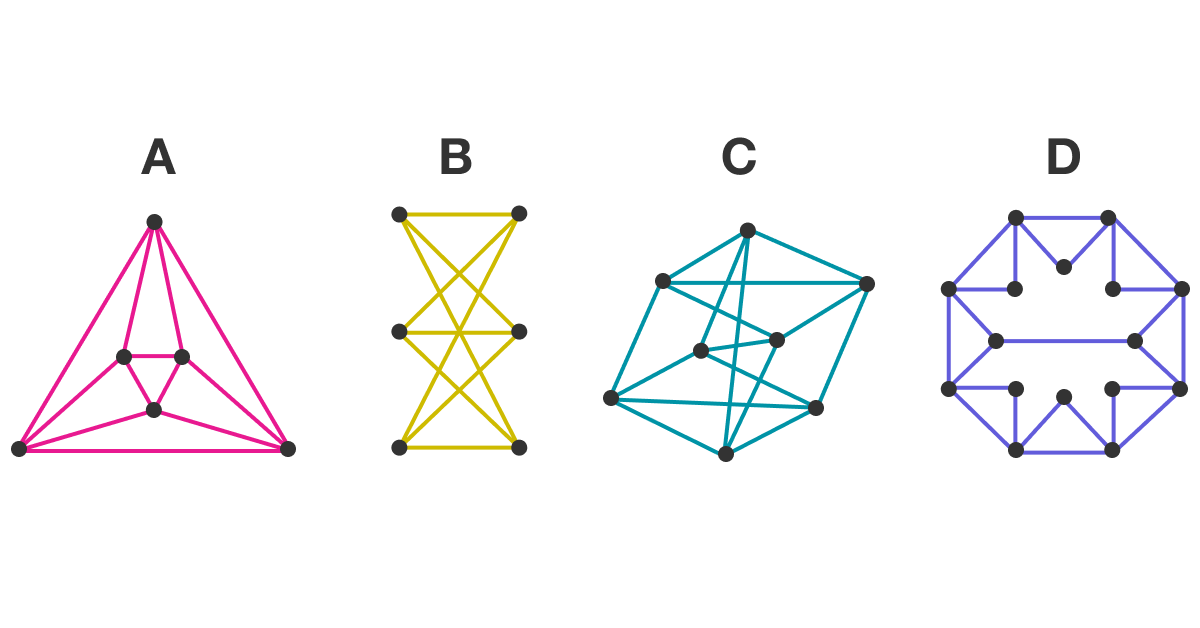 Which of the shapes above
cannot
be traced without lifting up your pencil and without tracing over the same edge twice?
Which of the shapes above
cannot
be traced without lifting up your pencil and without tracing over the same edge twice?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Can you provide any article about the proof of this?
Log in to reply
With a quick Google, I found this: http://www.math.uri.edu/~eaton/Euler.pdf .
Can you provide any article about the proof of this?
What kind of (math?) class could I learn about these types of things in?
I remembered this from topology many many years ago - you need to correct your spelling of Euler though!!!
Nice Pictures - but when you tried shape B (and failed), how do you know that you tried ALL possible paths - of did you use the Euler proof initially to know that B wasn't possible
Log in to reply
Thank you. To be honest, when I did this I didn't know about the Euler proof. I just tried tracing these shapes. After I found out how to trace shape A, D, then C, I knew that the answer was B. But in fact it didn't take me very long to trace these 3 shapes.
Did you write a program to draw these? Can someone tell me how to write such a program?
Graph B is not isomorphic but others are.
For this answer, I'm going to use the term order of a vertex to be the number of distinct edges that connect it. Do not confuse this term with the sequence of vertices to draw the graph.
Our goal is to trace each edge. Think about where each traced edge meets a vertex. If the order of the vertex is even, then we can trace through it until all the edges are "used up." The number of times tracing through a vertex is always n / 2 .
Note how after tracing through this order 4 vertex with orange:
We can trace through the same vertex again later without tracing the orange lines twice:
However, if the order of a vertex is odd (say 3), then when you arrive at the vertex the last time, there is nowhere to continue tracing.
Once we've traced the orange line, when we return to the vertex, there is nowhere to go!
We can now see that if a graph has a vertex with odd order, it must be either the end or the beginning of our sequence. This is the case with graph D, there are exactly two vertices with order 3, so when tracing this graph, those two vertices must be the start and end of the sequence.
However, in graph B, all six vertices have order 3. That means while tracing, we would end up getting stopped at a vertex, while at least one edge to 4 of the other vertices cannot have been visited (or we would have been stuck at one of those vertices instead.
Therefore, we cannot trace through Graph B .
The correct answer is B and D because for a graph to have an Euler walk (which is defined to be a walk that traverses every edge in a graph exactly once) you need to have an even degree on every vertex. Leave a comment if you're interested in the proof (it's a little longer)
If the graph can be traced without lifting the pencil, each vertex will have one edge going out for every edge going in, meaning that the number of edges connected to each vertex is even. Graph B does not satisfy this.
In order to be traceable, a graph cannot have more than two vertices where the number of edges leaving it is an odd number. For graph B, all six vertices have an odd number of edges leaving it, so it is not traceable.
From counting the order of each vertex, we can then sort each graph into 3 types: Eurlerian (all vertices are of even order), semi-Eurlerian (two of the vertices are of odd order) and non-Eurlerian (more than two of the vertices are of odd order).
From the definitions of each type of graph, a non-Eurlerian graph cannot create a Eulerian trail (a trail which visits every edge exactly once), because each edge adds two to the net order on all vertices (so you could go in, but not out of a vertex, sort of speak), so the answer is Graph B.
(Although, if graph B had only two odd vertices (a semi-Eurlerian graph), it would be possible for a Eurlerian trail, although the trail would have to start and finish at two distinct vertices.)
@Adam Blakey