Can linear equations be hard?
 Given that
Given that
f ( x ) = ∣ ∣ x ∣ − 1 ∣ P 0 ( x ) = f ( x ) P n + 1 ( x ) = f ( P n ( x ) )
A k = ∣ ∣ ∣ ∣ ∣ n → ∞ lim ∫ 0 k P n ( x ) − 0 . 5 d x ∣ ∣ ∣ ∣ ∣
A = max A k
And that k 0 is the minimum value such that A = A k 0 , where k ranges over all the positive reals k > 0 .
Find ⌊ 1 0 0 0 ( A + k 0 ) ⌋
Try my Other Problems
The answer is 625.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
So, I think you should define A k = ∣ lim ∫ 0 k … ∣ , and then A = min A k , and k 0 is the minimum value such that A = A k 0 .
That will clarify that the k in the integral is fixed as n tends to infinity, instead of being allowed to vary for different n .
Log in to reply
Or did you mean A = max A k ? I edited it already btw, thanks!
Just to elaborate a little
Let's take 2 Cases.
Case(1)
A k = ∣ ∣ ∣ 2 ⌊ k ⌋ + 2 { k } 2 − 2 k ∣ ∣ ∣ ⇒ A k = ∣ ∣ ∣ 2 { k } 2 − { k } ∣ ∣ ∣
Case(2)
A k = ∣ ∣ ∣ 2 ⌊ k ⌋ + 2 { k } ( 2 − { k } ) − 2 k ∣ ∣ ∣ ⇒ A k = ∣ ∣ ∣ 2 { k } − { k } 2 ∣ ∣ ∣
Note
The equations would remain same if k is odd or even.
Conclusion
A = ∣ ∣ ∣ 2 { k } 2 − { k } ∣ ∣ ∣ m i n = 8 1 a t { k } = 2 1 ⇒ k m i n p o s = k o = 2 1
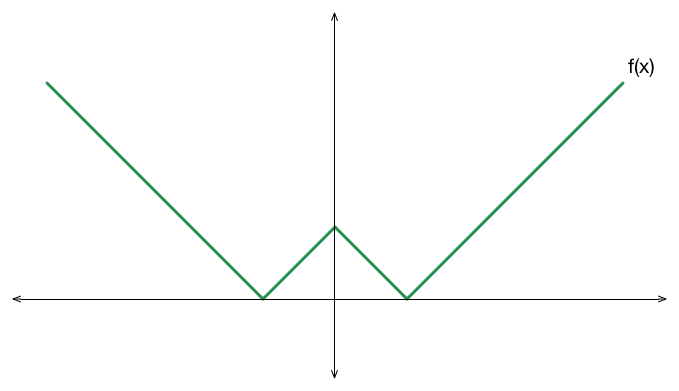
Consider the sketch of f ( x ) . It would be the graph ∣ x ∣ − 1 and then flipped upwards: hi
hi
Now consider f ( f ( x ) )
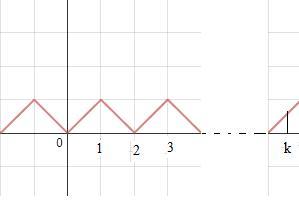
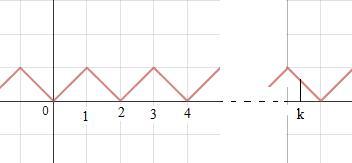
So for lim n → ∞ P n ( x ) − 0 . 5 , the graph would be either
or
Depending on whether n is odd or even.
It is now easy to see that the maximum of ∣ ∣ ∣ lim n → ∞ ∫ 0 k P n ( x ) − 0 . 5 d x ∣ ∣ ∣ is 0 . 5 2 / 2 = 0 . 1 2 5 = A and this occurs in either graph when x = 0 . 5 = k 0
Therefore, ⌊ 1 0 0 0 ( A + k 0 ) ⌋ = 6 2 5