Can the angle take on any value - 2
An isosceles trapezium has a perimeter of 8 0 , and an area of 2 5 0 . Let θ be the angle between any two adjacent sides. If the minimum of sin θ can be expressed as b a , where a and b are coprime positive integers, submit your answer as a + b .
Bonus: Do it for general isosceles trapezium!
Inspiration
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
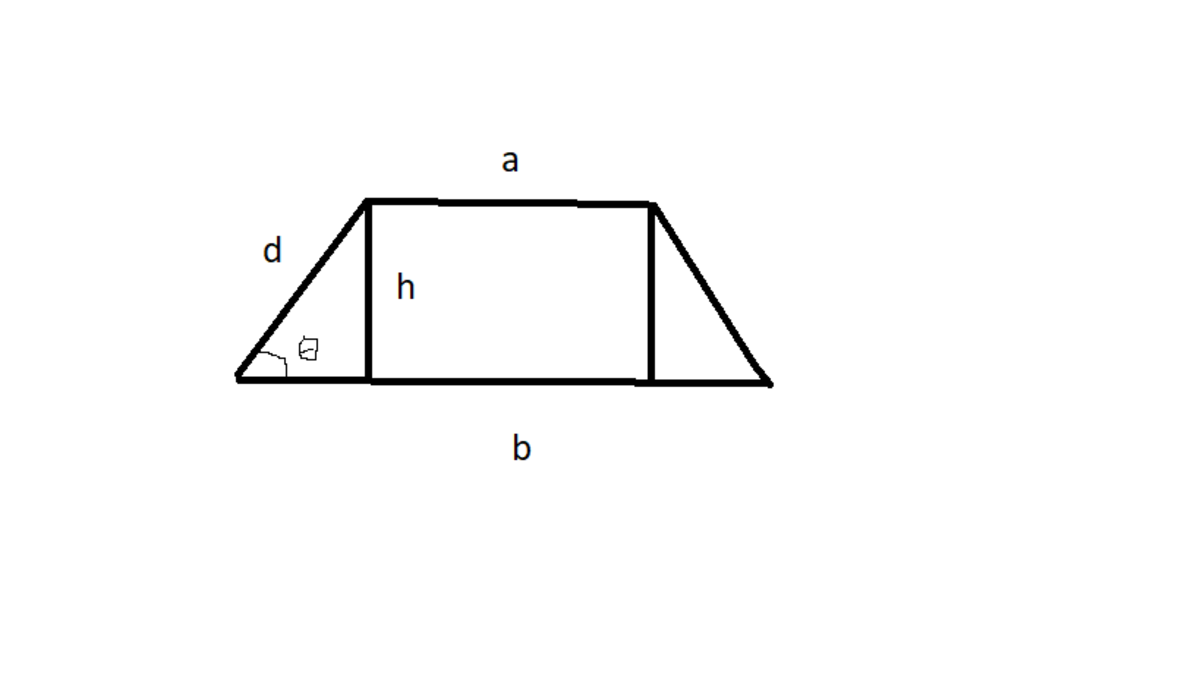 Label the two parallel sides as
a
and
b
respectively; also label the height as
h
. The hypotenuse of the right angled triangle is
d
=
sin
(
θ
)
h
. The area of a trapezium is given by
A
=
2
a
+
b
h
, while the perimeter for the isosceles trapezium is
P
=
2
d
+
a
+
b
.
Label the two parallel sides as
a
and
b
respectively; also label the height as
h
. The hypotenuse of the right angled triangle is
d
=
sin
(
θ
)
h
. The area of a trapezium is given by
A
=
2
a
+
b
h
, while the perimeter for the isosceles trapezium is
P
=
2
d
+
a
+
b
.
Using the area equation, we find that a + b = h 2 A . Substituting this into the perimeter equation along with the expression for d yields sin ( θ ) 2 h + h 2 A = P sin ( θ ) h = 2 P − h A = 2 h P h − 2 A sin ( θ ) = f ( h ) = P h − 2 A 2 h 2 Differentiate using the quotient rule: f ′ ( h ) = ( P h − 2 A ) 2 4 h ( P h − 2 A ) − 2 P h 2 = ( P h − 2 A ) 2 2 P h 2 − 8 A h Set the numerator to zero to find when f ′ ( h ) = 0 . 2 P h 2 − 8 A h = 2 h ( P h − 4 A ) = 0 ⟶ h = 0 , P 4 A Since h = 0 results in A = 0 , this is not a valid solution so h = P 4 A must be correct. Thus, the minimum of sin ( θ ) is: f ( P 4 A ) = P ( P 4 A ) − 2 A 2 ( P 4 A ) 2 = 2 A P 2 3 2 A 2 = P 2 1 6 A Substituting in P = 8 0 and A = 2 5 0 gives the final answer. 8 0 2 1 6 × 2 5 0 = 1 6 × 5 × 8 0 1 6 × 2 5 0 = 8 0 5 0 = 8 5 Therefore, a + b = 5 + 8 = 1 3 .
Any isosceles trapezoid can be associated with a parallelogram with the same perimeter, area, and angles. Just reflect half of the trapezoid across the midsegment that is parallel to the two bases. And the relationship works in reverse.
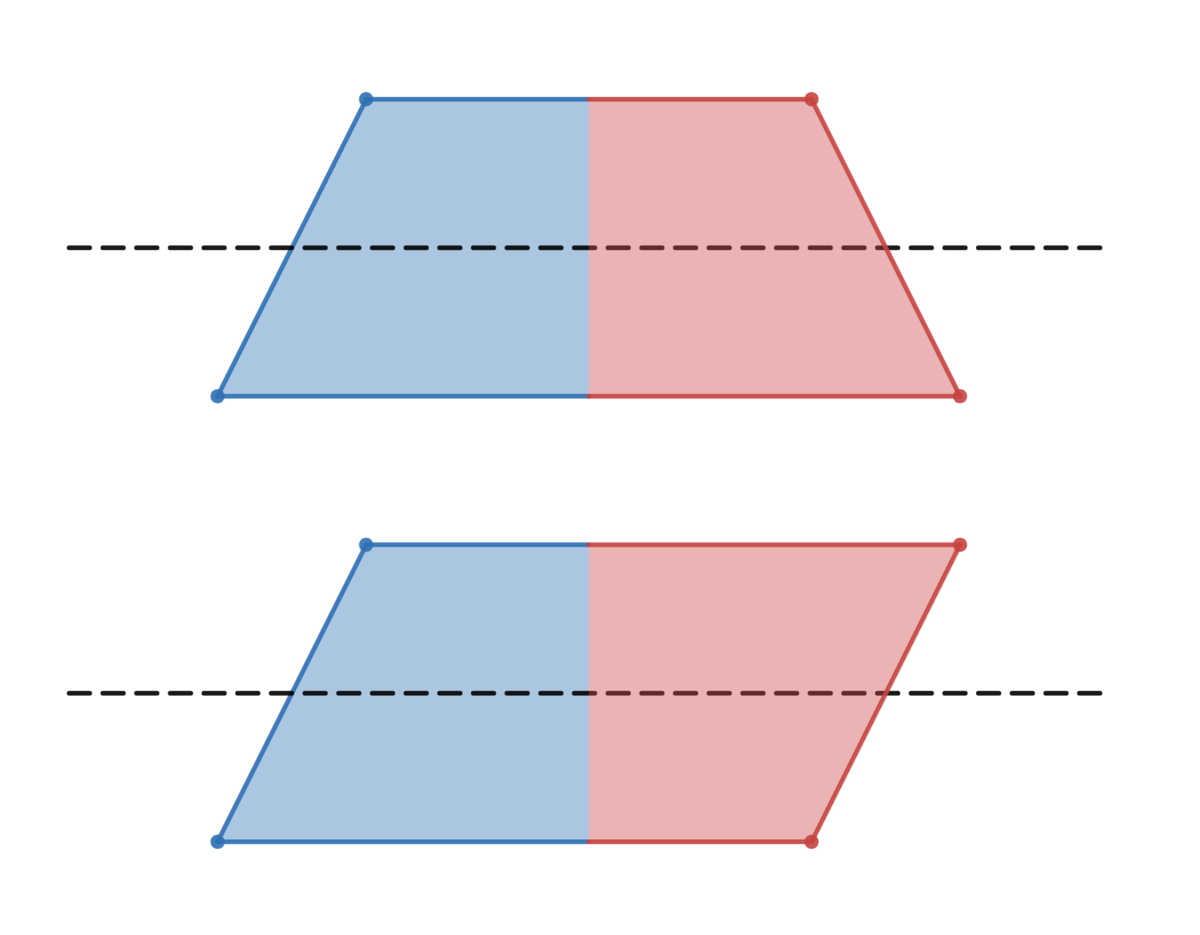 So the answer to this problem is the same as the minimum value of
sin
θ
in a parallelogram that meets the same criteria. That was the question addressed in the
Inspiration problem
, with general solution
sin
θ
≥
P
2
1
6
A
.
So the answer to this problem is the same as the minimum value of
sin
θ
in a parallelogram that meets the same criteria. That was the question addressed in the
Inspiration problem
, with general solution
sin
θ
≥
P
2
1
6
A
.
For the values given here, we get sin θ ≥ 8 0 2 1 6 ( 2 5 0 ) = 8 5 . So a + b = 5 + 8 = 1 3 .
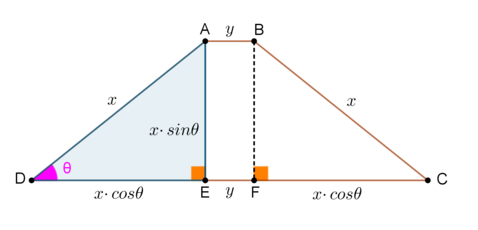 Denote by
P
the perimeter of trapezium
A
B
C
D
, by
A
its area and by
θ
the acute angle
∠
A
D
C
. Let
x
=
A
D
=
B
C
and
y
=
A
B
, the smaller of the two parallel sides of
A
B
C
D
. Let
E
,
F
be points on
C
D
such that
A
E
⊥
D
C
⊥
B
F
.
Then, we have the relations
Denote by
P
the perimeter of trapezium
A
B
C
D
, by
A
its area and by
θ
the acute angle
∠
A
D
C
. Let
x
=
A
D
=
B
C
and
y
=
A
B
, the smaller of the two parallel sides of
A
B
C
D
. Let
E
,
F
be points on
C
D
such that
A
E
⊥
D
C
⊥
B
F
.
Then, we have the relations
P = A D + B C + A B + D E = 2 x + 2 y + 2 x cos θ ⇒ 2 y = P − 2 x − 2 x cos θ ( 1 )
A = 2 1 ( A B + C D ) A E ⇒ 2 A = ( 2 y + 2 x cos θ ) x sin θ ⇒ ( 1 ) 2 A = ( P − 2 x − 2 x cos θ + 2 x cos θ ) x sin θ ⇒ ( 2 sin θ ) x 2 − ( P sin θ ) x + 2 A = 0
The latter is a quadratic equation which must have a solution for x , thus its discriminant must be non-negative, i.e.
Δ ≥ 0 ⇔ P 2 sin 2 θ − 1 6 A sin θ ≥ 0 ⇔ sin θ ( P 2 sin θ − 1 6 A ) ≥ 0 ⇔ 0 ∘ < θ < 9 0 ∘ P 2 sin θ − 1 6 A ≥ 0 ⇔ sin θ ≥ P 2 1 6 A
Hence, the minimum value for sin θ is ( sin θ ) min = P 2 1 6 A Substituting the specific values A = 2 5 0 and P = 8 0 , we get ( sin θ ) min = 8 0 2 1 6 × 2 5 0 = 8 5 .
Consequently, we find A D = B C = x = 2 0 , A B = y = 2 0 − 2 5 3 9 ≈ 1 2 . 2 and D C ≈ 2 7 . 8 .
For the answer, a = 5 , b = 8 , thus, a + b = 1 3 .

Area A = 2 1 ( B + b ) s sin ( θ ) = 2 5 0 ⟹ sin ( θ ) = ( B + b ) s 5 0 0
and
Perimeter P = B + b + 2 s = 8 0 ⟹ B + b = 8 0 − 2 s ⟹ sin ( θ ) = ( 4 0 − s ) s 2 5 0 ⟹ θ = arcsin ( 4 0 s − s 2 2 5 0 )
⟹ d s d θ = s ( 4 0 − s ) ( s 2 − 4 0 s − 2 5 0 ) ( s 2 − 4 0 s + 2 5 0 ) 5 0 0 ( s − 2 0 ) = 0
⟹ s = 2 0 and 5 ( 4 − 6 ) < s < 2 0 ⟹ d s d θ < 0 and 2 0 < s < 5 ( 4 + 6 ) ⟹ d s d θ > 0
⟹ a min occurs at s = 2 0 ⟹ sin ( θ ) = 4 0 0 2 5 0 = 8 5 = b a ⟹ a + b = 1 3 .
An isosceles trapezoid can be transformed into a parallelogram while keeping the same area and perimeter:
This problem is now the same as the inspiration problem , where it was found that sin θ ≥ P 2 1 6 A = 8 0 2 1 6 ⋅ 2 5 0 = 8 5 .
Therefore, a = 5 , b = 8 , and a + b = 1 3 .