Can the slope here can be found?
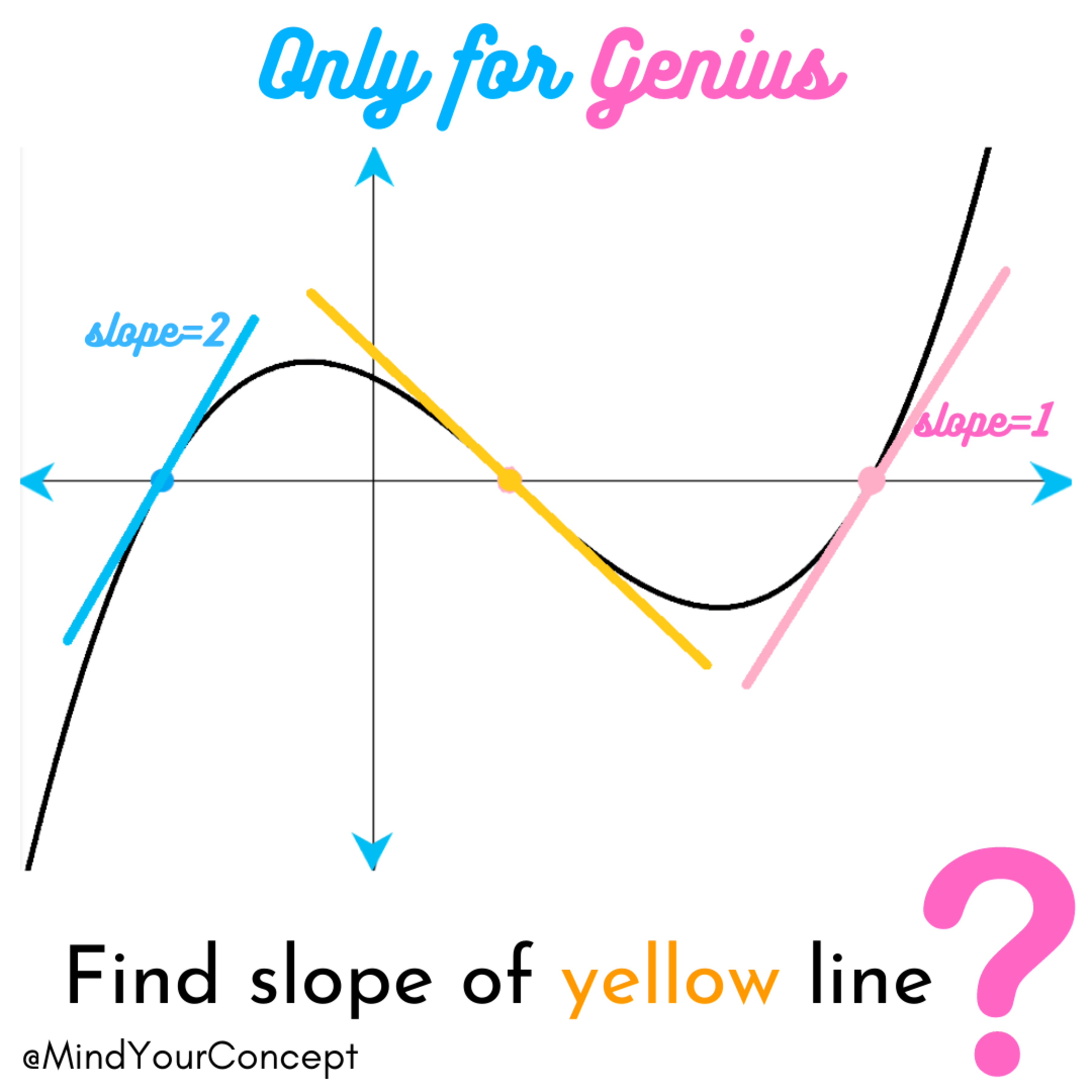
You are given a cubic curve and three slopes at its roots. The slopes denoted by the blue and pink lines are 2 and 1 respectively. Find the slope of yellow line?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
very nice sir!
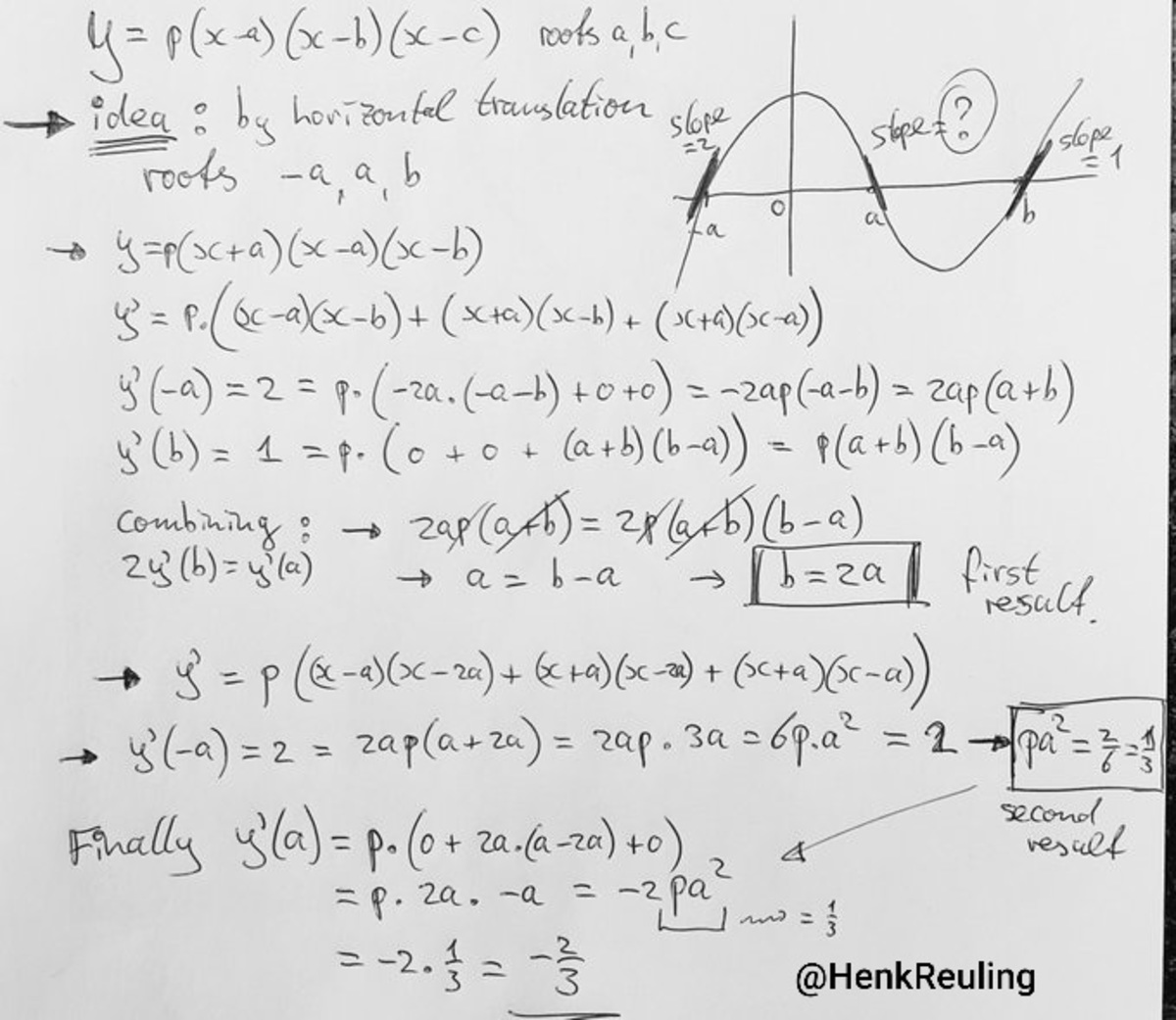
Nice solution. I think we can make the calculations slightly easier by assuming b = 0 (it's not a loss of generality as translating the graph left or right is not going to affect the slope).
f ( x ) = A ( x − a ) ( x − b ) ( x − c )
f ′ ( x ) = A ( x − b ) ( x − c ) + A ( x − a ) ( x − c ) + A ( x − a ) ( x − b )
f ′ ( a ) = A ( a − b ) ( a − c ) ,
f ′ ( b ) = A ( b − a ) ( b − c )
f ′ ( c ) = A ( c − a ) ( c − b )
f ′ ( a ) + f ′ ( c ) = A ( a − b ) ( a − c ) + A ( c − a ) ( c − b ) = A ( a − c ) ( a − b − c + b ) = A ( a − c ) 2
f ′ ( a ) f ′ ( c ) = A ( a − b ) ( a − c ) A ( c − a ) ( c − b ) = − A 2 ( a − c ) 2 ( a − b ) ( c − b ) = − ( A ( b − a ) ( b − c ) ) ( A ( a − c ) 2 ) = − f ′ ( b ) ( f ′ ( a ) + f ′ ( c ) )
So f ′ ( b ) = − f ′ ( a ) + f ′ ( c ) f ′ ( a ) f ′ ( c ) = − 1 + 2 1 ∗ 2 = − 3 2
According to the first solution, the polynomial has complex coefficients, and two complex roots(zeroes of the polynomial). So, the plot is on the complex plane.
The first thing that came to my mind: derivative! Second: root! Third: QUIT! The formula is too long :P

Let the cubic function be f ( x ) and its three real roots be a , b , and c such that a < b < c . Then we have:
f ( x ) ⟹ f ′ ( x ) f ′ ( a ) f ′ ( c ) f ′ ( a ) + f ′ ( c ) ⟹ f ′ ( b ) = ( x − a ) ( x − b ) ( x − c ) = ( x − b ) ( x − c ) + ( x − a ) ( x − c ) + ( x − a ) ( x − b ) = ( a − b ) ( a − c ) = a 2 − a b + b c − c a = 2 = ( c − a ) ( c − b ) = c 2 + a b − b c − c a = 1 = a 2 + c 2 − 2 c a = ( c − a ) 2 = 3 = ( b − a ) ( b − c ) = − ( c − a ) 2 ( a − b ) ( a − c ) ( c − a ) ( c − b ) = − 3 f ′ ( a ) f ′ ( c ) = − 3 2 ⋅ 1 = − 3 2 Slope of the blue line Slope of the pink line Slope of the yellow line Note that ( c − a ) 2 = 3