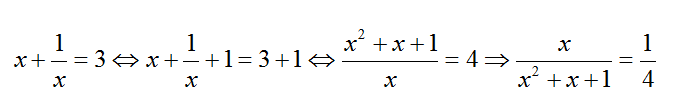Consider The Reciprocal First!

$\frac{x}{1+x+x^2 }$

Dividing numerator and denominator by x and noting that x $\neq 0$ ,

$= \frac{1}{ \frac{1}{x} + 1 + x}$

$= \frac{1}{3+1}$

$= \frac{1}{4}$

By re-arranging the first formula we get

$x^2 + 1 = 3x$

If we add $x$ to that we get

$1 + x + x^2 = 4x$

That's the same as the bottom of the second equation, this means we can substitute it in

$\frac{x}{1 + x + x^2} \Rightarrow \frac{x}{4x}$

Cancelling the $x$ 's gives us

$\frac{x}{4x} = \boxed{\frac{1}{4}}$

$\frac {x}{1+x+x^2} = \left(\frac{1+x+x^2}{x}\right)^{-1} = \left(\frac{1}{x} + 1 + x\right)^{-1} = (1+3)^{-1} = 4^{-1} = \frac{1}{4}$

x+1/x=3
---> x^2+1=3x
--->x^2+x+1=4x
--->(x^2+x+1)/x=4
--->x/(x^2+x+1)=1/4

multiply out by x. so, $x^{2} + 1 = 3x$ . now add x. so, we now have, $x^{2} +x + 1=4x$ .

x/ $[1+x+x^{2}]$ = x/4x = 1/4

x+1/x=3 by solving it we get thatx^2+1=3x by substituitindsubstituiting in given equation we get answer is 1/4