Can we find its velocity?

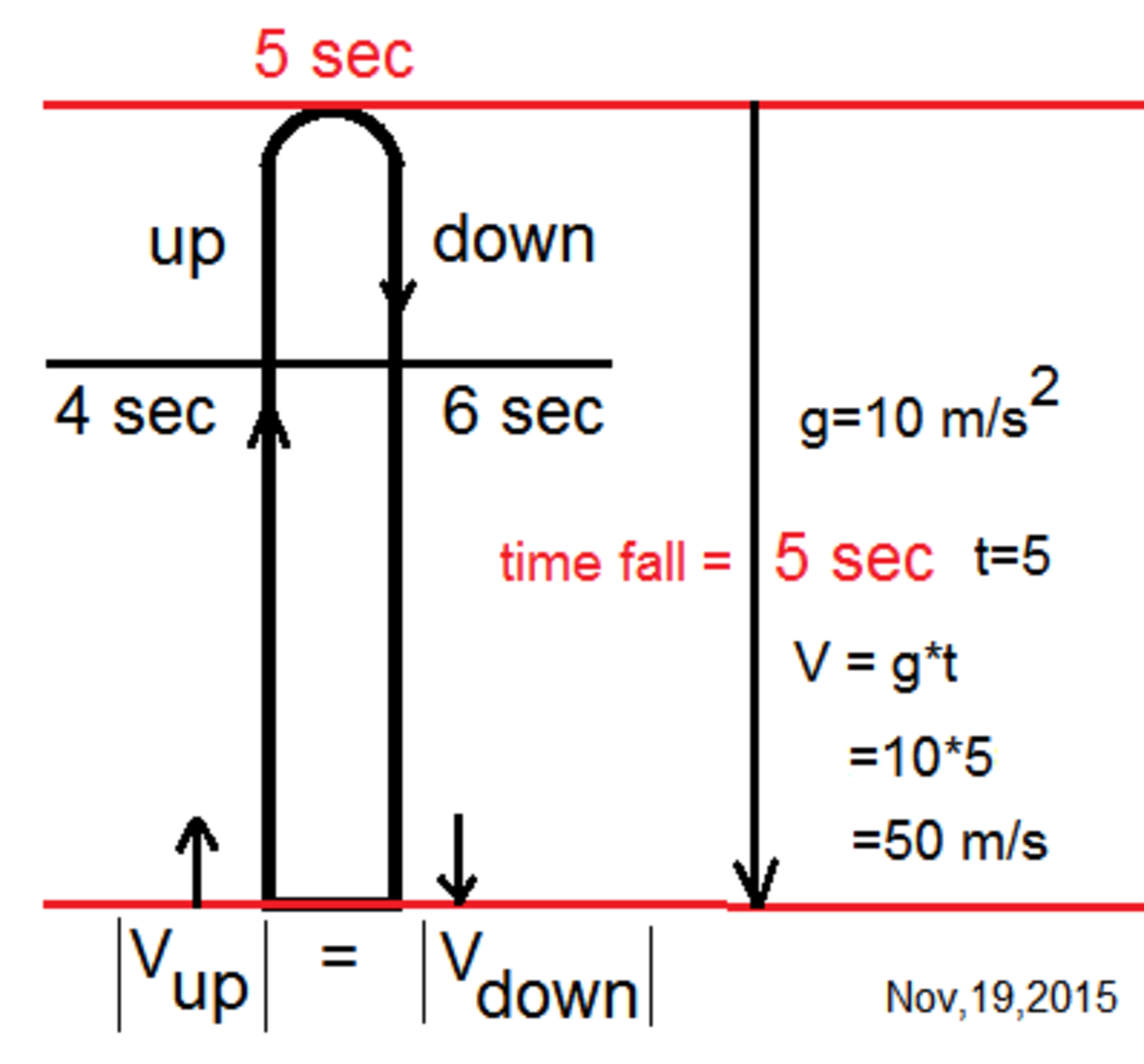
Assuming that the motion is entirely vertical, the height $y$ of the ball (in $m$ ) will be given by the equation

$y = vt - \dfrac{g}{2}t^{2} = vt - 5t^{2},$

where $v$ is the initial upward velocity and where we have taken $g$ to be $10 m/s^{2}$ as suggested. Now for the ball to be at the same height at both $t = 4 s$ and $t = 6 s$ we will require that

$4v - 5*4^{2} = 6v - 5*6^{2} \Longrightarrow 4v - 80 = 6v - 180 \Longrightarrow 100 = 2v \Longrightarrow v = \boxed{50 m/s}.$

The ball is at the same height after 4 and 6 seconds, on the 5th second it was in the maximum height, and in the maximum height the ball's velocity is 0, if V=Vi-A.T and V=0, 0=Vi-A.T, 0=Vi-5.10, Vi=50

Since the ball is at the same height after both 4 seconds and 6 seconds, we can conlude that the ball reached its maximum height after 5 seconds. When the ball is at its maximum height, the velocity at that point is zero. Using the formula vf = vi + at and substituting t=5, vf=0, and a = -10. The equation becomes 0 = vi - (10)(5), therefore vi = 50 m/s