Can we reach escape velocity ?
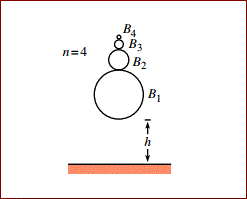 On a basketball is kept another basketball of smaller size, on which a tennis ball is kept on which is a smaller ball, and so on and so forth. If the balls are released with the largest ball at height
h
, find minimum number of balls so that after the collision, the smallest ball reaches the escape velocity.
On a basketball is kept another basketball of smaller size, on which a tennis ball is kept on which is a smaller ball, and so on and so forth. If the balls are released with the largest ball at height
h
, find minimum number of balls so that after the collision, the smallest ball reaches the escape velocity.
Note: Work in the approximation where m 1 (mass of the biggest ball) is much larger than m 2 , which is much larger than m 3 , etc., and assume that the balls bounce elastically.
Assumptions and Details
- Assume r i ≪ h
- Radius of Earth = 6.4 X 1 0 6 m
- h = 1 m
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
For Simplicity, Let us assume there is a very small distance, so that the relative bounces happen after a short time interval. Just before collision with the ground, both balls are moving with same velocity i.e. v = 2 g h Just after collision, the basket ball is coming up with velocity v and the upper ball is coming down with velocity v. The relative speed them is therefore 2v. After the balls bounce off each other, the relative speed is still 2v. (This is clear if you look at things in the frame of the basketball, which is essentially a brick wall.) Since the upward speed of the basketball essentially stays equal to v (it is like a big ball with little effect of collision) , the upward speed of the tennis ball is 2v + v = 3v Similarly the velocity of third ball will be (3v + v) + v = 7v. Similarly, the velocity of (i+1)th ball would be v i + v + v i = 2 v i + v. Using concepts of Sequences and Series, we find v n = ( 2 n - 1 )v
To reach escape velocity, v n >= 2 g R . From this we find n = 1 3 . Of course, the elasticity assumption is absurd in this case, as is the notion that one can find 13 balls with the property that m 1 ≫ m 2 ≫ … m 1 2 .
If you like the problem and solution, plz follow me. The problem is not mine, but the solution is mine.
Any better solution is welcomed.
n
=
l
o
g
(
2
)
l
o
g
(
R
+
1
)
≈
1
1
.
3
b
a
l
l
s
n
=
1
2
b
a
l
l
s
n = l o g ( 2 ) l o g ( R + 1 ) ≈ 1 1 . 3 b a l l s
n = 1 2 b a l l s