Can we think out of the box?

The reason why we cannot have a platonic solid with six equal sides (regular hexagon) on each of its surface is because:

• A) A regular hexagon has internal angles of $120^\circ$ , but $3\times120^\circ=360^\circ$ (angle of the point at which three sides, one from each surface will meet) which won't work because at $360^\circ$ the shape flattens out.

• B) It is possible, as it does not depend upon the internal angles rather depends upon the angles made by one surface to other.

• C) It is possible, as while forming a polyhedron it neither depends upon the internal angle nor on the mutual angles between the surface.

• D) None of the above.

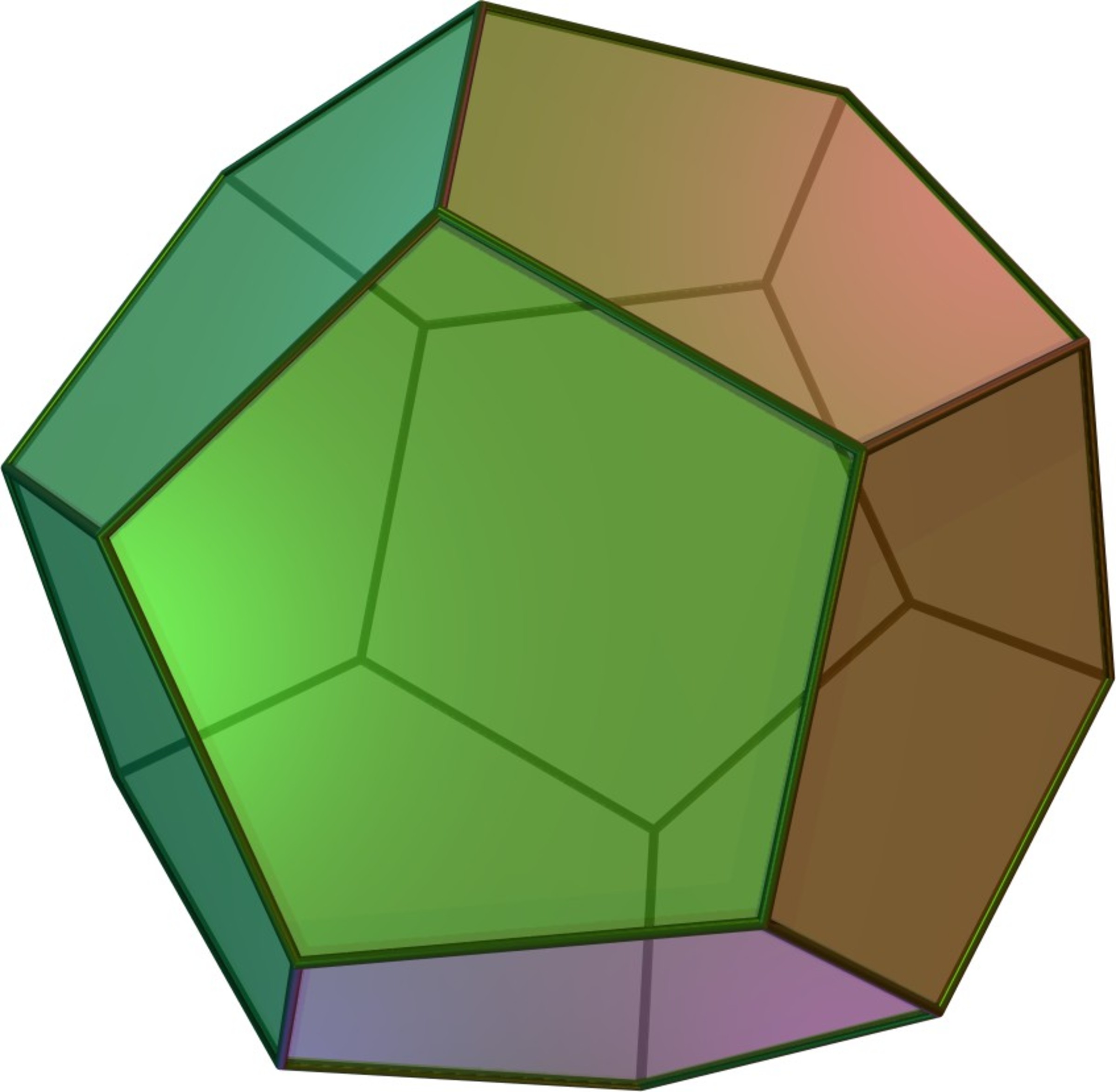
Assumption: A Regular dodecahedron as shown above, has 5 equal sides (regular pentagon) on each of its surface, like wise the question asks the reason behind the impossibility of a polyhedron with six equal side on each of its surface.