Can We Trust Her?

Geometry Level 1

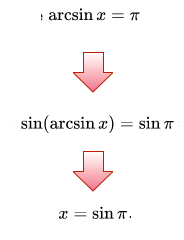
Michaelle asked the classroom to solve $\arcsin x=\pi$ for $x$ . After some minutes, she wrote the equation on the blackboard. She solved it as follows:

"Due to the fact that the arcsine of $x$ is defined as the inverse sine function of $x$ , we can write $\sin\left(\arcsin x\right)=\sin\pi \Rightarrow x=\sin\pi$ . We have that $\sin\pi=0$ , so the unique solution to this equation is $x=0$ ."

Is this reasoning correct?

Yes No

1 solution

Ivan Koswara
Apr 13, 2016

The definition of $\arcsin x$ (for real $x$ ) is the value $y$ in the interval $\left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]$ such that $\sin y = x$ . Since $\pi$ is outside that interval, by definition there is no $x$ that will give $\arcsin x = \pi$ . The reason that the extraneous solution $x = 0$ is obtained is because $\sin \pi = 0$ ; however, we also have $\sin 0 = 0$ , so $\arcsin 0 = 0$ instead of $\arcsin 0 = \pi$ .

Moderator note:

Great explanation! We have to be aware of the domain (and range) of these functions for their inverses to be defined.

Can We Trust Her?

1 solution

Moderator note:

0 pending reports