Can We Use Parity?
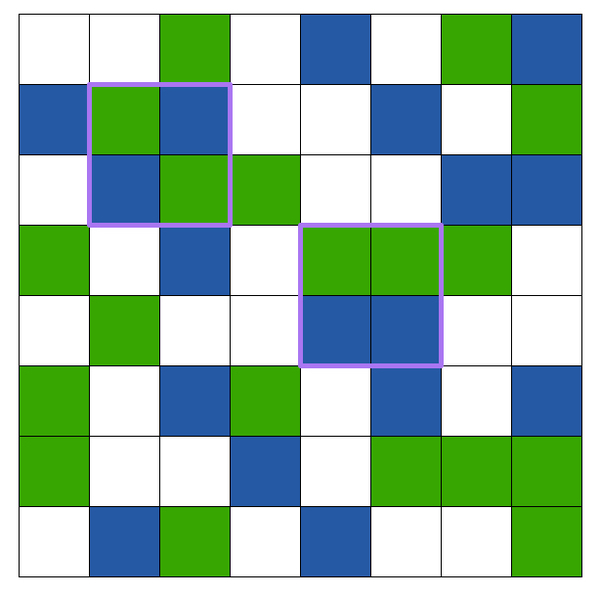
Consider an grid of squares. We color every square blue or green such that 3 of the 4 squares on the corners of the grid are blue and the fourth is green.
Will there always exist a square inside this grid such that there are an odd number of squares of each color inside?
Bonus: Generalize this for the grid.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
What a great problem! (+1)
Lets assume you can paint the n × n grid so that every 2 × 2 grid has an even number of blue squares. And prove by contradiction that there must be at least one "odd parity" 2 × 2 grid.
And for now, lets assume n = 1 0 , although you'll see pretty quickly that the same argument is valid for all n > 1 .
Consider the squares numbered as they are in this picture:
Now consider the 2 × 2 grid in the lower left corner (81,82,91,92). It must have an even number of blue squares. Now consider the 2 × 2 grid (71,72,81,82) which also must have an even number of blue squares (or even parity). From these two facts you can conclude that the four squares (71,72,91,92) also must have even parity. A similar argument implies that (61,62,91,92) has even parity, and this can be continued vertically until you see that (1,2,91,92) have even parity.
Now, continuing this argument horizontally, (1,3,91,93) must have even parity, as would (1,4,91,94). Continuing this argument to the boundaries of the 1 0 × 1 0 grid, this would imply that (1,10,91,100) would necessarily have even parity.
However, since the corners have odd parity (1 is one color and 3 are another) then we have a contradiction.
Therefore, we can't cover the array with with 2 × 2 grids of even parity, so, yes we can always find an odd parity 2 × 2 grid in there somewhere! :0)
Clearly, we didn't use the fact that we took n = 1 0 anywhere in the argument, so this argument is valid for all n > 1 .