Can you solve this IT puzzle?

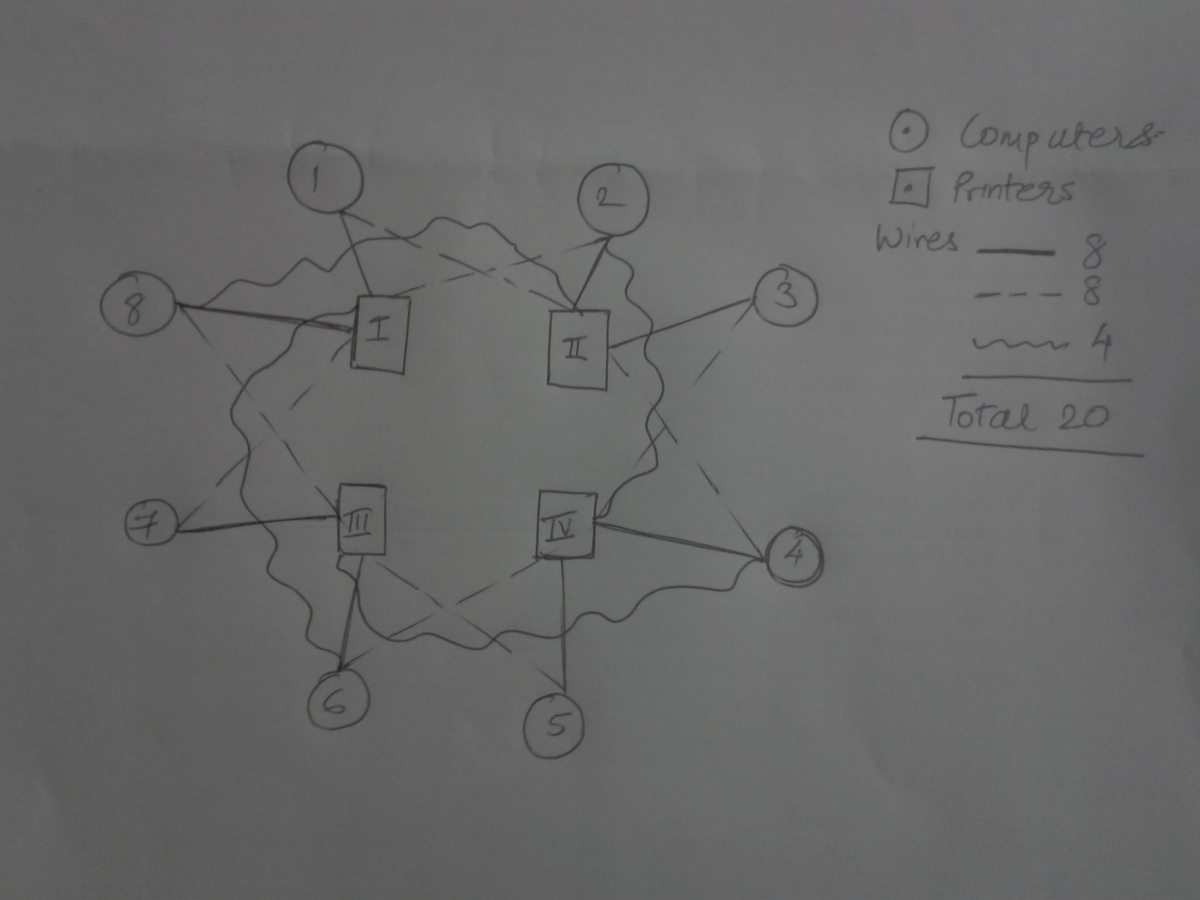
First, I claim that $20$ cables work.

Number the computers $1, 2, \ldots, 8$ and the printers $1, 2, 3, 4$ . Connect computer $i$ to printer $i$ for all $i \in \{1, 2, 3, 4\}$ . Connect the four other computers to all four printers. Now, given four selected computers, process the first four computers first: they have only one printer to go. The remaining computers have free choices, and can obviously be fitted to all printers.

Now, I claim that $19$ cables doesn't work.

By Pigeonhole Principle, with $19$ cables and $4$ printers, one printer is connected to at most $4$ computers. Pick four computers not connected to this printer. They collectively cannot use this printer, so there are four computers and three printers, impossible to complete.

The problem actually becomes a lot simpler if you consider it from the perspective of the printers, rather than the computers: each printer needs to be connected to some subset of the computers such that for any combination of four computers, each printer is connected to at least one of them.

Each printer then needs to be connected to at least five of the eight computers: so a total of 5*4 = $\boxed{20}$ cables are needed.

$\text{n!-n}$ .

$\text{4!=24}$ .

$\text{24-4=20}$ .

Hence the answer is $\boxed{20}$ .