Can you count all these oranges?
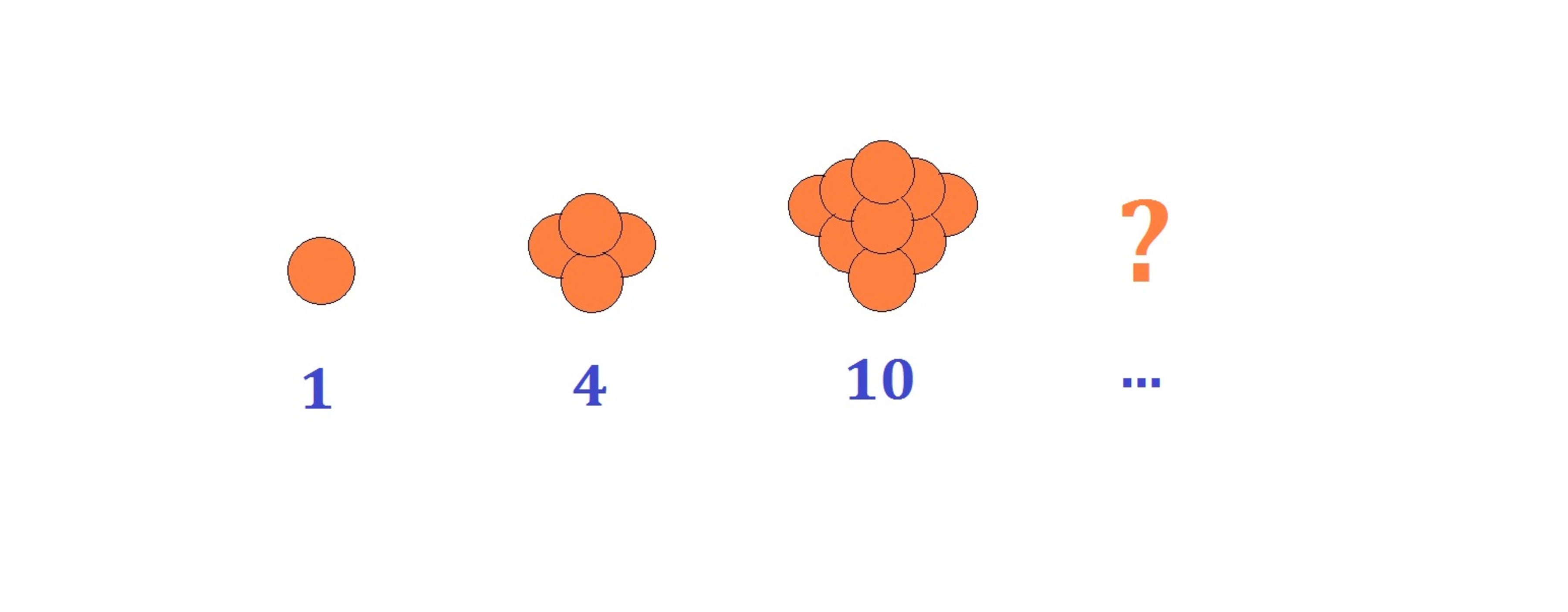
The oranges are arranged so that there is 1 top orange; the second top layer has 2 more oranges than the top; the third has 3 more oranges than the second, and so on. Forming a tetrahedron of oranges, this "tetrahedral" number of oranges runs as a series as shown above.
What is the value of the term of this series?
The answer is 171700.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
When we separate this sequence by parts or layers of the oranges, we will see a pattern as shown:
a 1 = 1
a 2 = 1 + 3 = 1 + (1 + 2)
a 3 = 1 + 3 + 6 = 1 + (1 + 2) + (1 + 2 + 3)
...
a n = 1 + (1 + 2) + (1 + 2 + 3) + ... + (1 + 2 + 3 + ... + n)
So we can see that this series is, in fact, a sum of sums of all natural numbers under n.
That is, a n = ∑ ( ∑ n ) = ∑ ( 2 n ( n + 1 ) ) as we know that the sum of 1 to n equals to 2 n ( n + 1 ) from the formula.
Now a n = ∑ ( 2 n ( n + 1 ) ) = 2 1 [ ∑ n 2 + ∑ n ]
From the formulas, ∑ n 2 = 6 n ( n + 1 ) ( 2 n + 1 ) and again ∑ n = 2 n ( n + 1 ) , we will get:
a n = 2 1 [ ∑ n 2 + ∑ n ] = 2 1 [ 6 n ( n + 1 ) ( 2 n + 1 ) + 2 n ( n + 1 ) ]
= 2 1 [ 6 n ( n + 1 ) ( 2 n + 1 + 3 ) ] = 2 1 [ 6 n ( n + 1 ) ( 2 n + 4 ) ] = 6 n ( n + 1 ) ( n + 2 )
Therefore, a 1 0 0 = 6 1 0 0 ( 1 0 0 + 1 ) ( 1 0 0 + 2 ) ) = 1 7 1 , 7 0 0 .
As a result, there will be 1 7 1 , 7 0 0 oranges when 100 layers of oranges are made.