Can you count all these oranges?

Probability Level 2

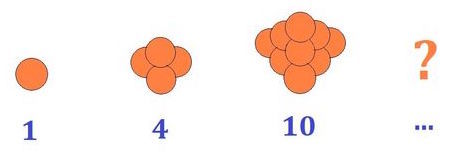
The oranges are arranged such that there is 1 top orange; the second top layer has 2 more oranges than the top; the third has 3 more oranges than the second, and so on. Forming a tetrahedron of oranges, these "tetrahedral" numbers of oranges run as a series, as shown above.

What is the value of the 10 0 th 100^{\text{th}} term of this series?


The answer is 171700.

Worranat Pakornrat by Worranat Pakornrat , 36, Thailand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

When we separate this sequence by parts or layers of the oranges, we will see a pattern as shown:

a 1 a_{1} = 1

a 2 a_{2} = 1 + 3 = 1 + (1 + 2)

a 3 a_{3} = 1 + 3 + 6 = 1 + (1 + 2) + (1 + 2 + 3)

...

a n a_{n} = 1 + (1 + 2) + (1 + 2 + 3) + ... + (1 + 2 + 3 + ... + n)

So we can see that this series is, in fact, a sum of sums of all natural numbers under n.

That is, a n a_{n} = ∑ ( ∑ n \sum (\sum n ) = ∑ ( n ( n + 1 ) 2 \sum (\frac{n(n+1)}{2} ) as we know that the sum of 1 to n equals to n ( n + 1 ) 2 \frac{n(n+1)}{2} from the formula.

Now a n a_{n} = ∑ ( n ( n + 1 ) 2 \sum (\frac{n(n+1)}{2} ) = 1 2 \frac{1}{2} [ ∑ n 2 \sum n^2 + ∑ n \sum n ]

From the formulas, ∑ n 2 \sum n^2 = n ( n + 1 ) ( 2 n + 1 ) 6 \frac{n(n+1)(2n+1)}{6} and again ∑ n \sum n = n ( n + 1 ) 2 \frac{n(n+1)}{2} , we will get:

a n a_{n} = 1 2 \frac{1}{2} [ ∑ n 2 \sum n^2 + ∑ n \sum n ] = 1 2 \frac{1}{2} [ n ( n + 1 ) ( 2 n + 1 ) 6 \frac{n(n+1)(2n+1)}{6} + n ( n + 1 ) 2 \frac{n(n+1)}{2} ]

= 1 2 \frac{1}{2} [ n ( n + 1 ) ( 2 n + 1 + 3 ) 6 \frac{n(n+1)(2n+1+3)}{6} ] = 1 2 \frac{1}{2} [ n ( n + 1 ) ( 2 n + 4 ) 6 \frac{n(n+1)(2n+4)}{6} ] = n ( n + 1 ) ( n + 2 ) 6 \frac{n(n+1)(n+2)}{6}

Therefore, a 100 a_{100} = 100 ( 100 + 1 ) ( 100 + 2 ) 6 \frac{100(100+1)(100+2)}{6} = 171,700.

As a result, there will be 171,700 oranges when 100 layers of oranges are made.

9 Helpful 0 Interesting 0 Brilliant 0 Confused

Or you can just apply Hockey Stick Identity : ∑ n = 1 100 ( n + 1 2 ) = ( 100 + 2 3 ) = 171700 . \sum_{n=1}^{100} \dbinom{n+1}2 = \dbinom{100 + 2}3 = \boxed{171700}.

Pi Han Goh - 5 years, 6 months ago

Log in to reply

Oh, there's a name for this. I didn't know. Lol...

Worranat Pakornrat - 5 years, 6 months ago

But according to the question, shouldn't the 2nd layer have 3 oranges??

Yuki Kuriyama - 5 years, 6 months ago

Log in to reply

Yes, the second layer has 3 oranges, and the third has 6 oranges.

Worranat Pakornrat - 5 years, 6 months ago

This was my solution. But I like Pi Han Goh's more.

Let x x be our sum. Then I figured that

x = 1 ( 2 ) 2 + 2 ( 3 ) 2 + 3 ( 4 ) 2 + 4 ( 5 ) 2 + ⋯ + 99 ( 100 ) 2 + 100 ( 101 ) 2 x = \frac{1(2)}{2} + \frac{2(3)}{2} + \frac{3(4)}{2} + \frac{4(5)}{2} + \cdots + \frac{99(100)}{2}+\frac{100(101)}{2}

x = 2 ( 1 + 3 ) 2 + 4 ( 3 + 5 ) 2 + 6 ( 5 + 7 ) 2 + 8 ( 7 + 9 ) 2 + ⋯ + 98 ( 97 + 99 ) 2 + 100 ( 99 + 101 ) 2 x = \frac{2(1+3)}{2} + \frac{4(3+5)}{2} + \frac{6(5+7)}{2} + \frac{8(7+9)}{2} + \cdots + \frac{98(97+99)}{2}+\frac{100(99+101)}{2}

x = ( 1 + 3 ) + 2 ( 3 + 5 ) + 3 ( 5 + 7 ) + 4 ( 7 + 9 ) + ⋯ + 49 ( 97 + 99 ) + 50 ( 99 + 101 ) x = (1+3) + 2(3+5) + 3(5+7) + 4(7+9) + \cdots + 49(97+99)+ 50(99+101)

x = 1 ⋅ 4 + 2 ⋅ 8 + 3 ⋅ 12 + 4 ⋅ 16 + ⋯ + 49 ⋅ 196 + 50 ⋅ 200 x = 1 \cdot 4 + 2 \cdot 8 + 3 \cdot 12 + 4 \cdot 16 + \cdots + 49 \cdot 196+ 50 \cdot 200

x = 4 ⋅ [ 1 2 + 2 2 + 3 2 + 4 2 + ⋯ + 4 9 2 + 5 0 2 ] x = 4 \cdot [1^{2} + 2^{2} + 3^{2} + 4^{2} + \cdots + 49^{2}+ 50^{2}]

x = 4 ⋅ [ 50 ⋅ 51 ⋅ 101 6 ] x = 4 \cdot [\frac{50 \cdot 51 \cdot 101}{6}]

x = 4 ⋅ [ 50 ⋅ 51 ⋅ 101 6 ] x = 4 \cdot [\frac{50 \cdot 51 \cdot 101}{6}]

x = 171700 x = \boxed{171700}

Patrick Engelmann - 5 years, 6 months ago
Andy Hayes
Nov 7, 2016

Each layer of oranges is a triangular number. Triangular numbers can be computed with the binomial coefficient.

∑ k = 1 n k = ( n + 1 2 ) \sum\limits_{k=1}^{n}{k}=\binom{n+1}{2}

The sum of triangular numbers can be computed with the hockey stick identity .

∑ k = 1 n ∑ j = 1 k j = ∑ k = 1 n ( k + 1 2 ) = ( n + 2 3 ) \sum\limits_{k=1}^{n}\sum\limits_{j=1}^{k}{j}=\sum\limits_{k=1}^{n}\binom{k+1}{2}=\binom{n+2}{3}

So the sum of the first 100 triangular numbers is:

∑ k = 1 100 ∑ j = 1 k j = ( 102 3 ) = 171700 \sum\limits_{k=1}^{100}\sum\limits_{j=1}^{k}{j}=\binom{102}{3}=\boxed{171700}

6 Helpful 0 Interesting 0 Brilliant 0 Confused
Ariella Lee
Dec 9, 2015

I counted layer by layer, just like Worranat Pakornrat, but calculated the sum a different (sort of) way.

The top layer has 1 1 orange. The next layer as 1 1 orange in its first row, then 2 2 oranges in its second row, so 1 + 2 1+2 oranges. The third layer has 1 + 2 + 3 1+2+3 oranges. And so on. The 100 100 th layer will have 1 + 2 + ⋯ + 100 1+2+\cdots+100 oranges.

So we want to compute: 1 + ( 1 + 2 ) + ( 1 + 2 + 3 ) + ⋯ + ( 1 + 2 + ⋯ + 100 ) 1+(1+2)+(1+2+3)+\cdots+(1+2+\cdots+100) . There are 100 100 ones, 99 99 twos, 98 98 threes, and so on, so we have: ( 1 ⋅ 100 ) + ( 2 ⋅ 99 ) + ( 3 ⋅ 98 ) + ⋯ + ( 100 ⋅ 1 ) (1\cdot100)+(2\cdot99)+(3\cdot98)+\cdots+(100\cdot1) . This can be represented by ∑ k = 1 100 k ( 101 − k ) \sum_{k=1}^{100}k(101-k) , which I used the computer calculate, or you can write it as 101 ∑ k = 1 100 k − ∑ k = 1 100 k 2 101\sum_{k=1}^{100}k-\sum_{k=1}^{100}k^{2} and use the formulas.

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Nikola Djuric
Dec 14, 2015

S=1+(1+2)+(1+2+3)+...+(1+...+100)= 100×1+(100-1)×2+...(100-99)×100= 100×(1+2+...+100)-1x2-2x3-..-99×100= 100×100×101/2-2(1+(1+2)+(1+2+3)+ ...+(1+2+3+...+99))= 100²×101/2-2(S-100×101/2) So 3S=100²×101/2+100×101= 100×101×(100+2)/2 So S=100×101×102/6=171700

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...