It's 1944 And Nazis Are About To Retaliate. Can You Crack This Code In Time?

I believe there are far more elegant ways to decode the Vigenère cipher, but here is my approach which is more like a bad episode of Law and Order than a beautiful algorithmic solution. I used Mathematica for my work.

First, I wrote a function to sample the characters of the cipher text (cipherText) according to different periods, $n$

charactersSample[n_] := Transpose@Partition[Characters@cipherText, n];

I use this function to take periodic samples of the text to evaluate as potential shifts.

As indicated in the problem, an easy thing to do is a frequency analysis. Natural languages have a structure to them that reflects common usage patterns. For instance, in English, the letters e, t, and a are boosted in comparison to the rest of the alphabet, and the letters x, z, q, and j are very rare compared to the rest of the alphabet

If we pick the wrong key length for the cipher text and analyze letter frequency, we can expect that the frequencies for the rarest letters will be boosted compared their frequencies for a correct key length (those letters will have low frequencies from their occasional appearance in the correct sampling as it comes in and out of frame with the erroneous key length we pick). Similarly, the letters that represent e, t, and a will be artificially lowered as they mix with out of frame sampling.

This should tend to make the letter distribution more linear and destroy the rich structure found in the natural usage.

A shift of $n$ results in $n$ sub-cipher texts, each with a characteristic letter distribution. In order to find the right key length for the encrypted text, I computed the average letter distribution vector (after sorting each vector by value) for each key length, took the mean of the $n$ vectors (to establish an average letter frequency vector for the given key length) and plot them all with the frequency vector for the English language.

It appears that the letter frequency vector for a key length of five (green) maintains the structure of the natural language (blood orange), whereas the other key lengths are linearized by the sampling.

To confirm the finding above, I took the mean letter frequency vectors for key lengths from 2 to 30 and took their inner product with the sorted letter frequency vector for the English language:

The inner product has peaks at key lengths which are multiples of 5.

This suggests that the key length is indeed 5.

Now, we look at the frequency tables of the sub-cipher texts for the key length 5:

L   23  M   27  I   25  T   32  S   27
A   21  Q   22  T   24  I   23  H   24
Z   20  A   20  C   22  P   22  B   24
H   20  W   18  X   21  X   21  C   23
V   19  V   16  H   20  D   20  G   18
U   17  I   16  G   17  C   19  O   16
P   16  Z   12  P   15  H   18  D   14
T   13  B   12  D   15  B   13  W   13
Y   12  X   10  N   10  G   11  A   10
K   12  K   10  K   7   R   7   Q   9
O   10  T   9   J   7   N   7   M   9
F   8   U   8   E   7   A   6   Z   6
W   7   J   7   A   7   V   5   V   5
M   6   P   6   W   6   K   5   J   5
C   5   L   6   B   6   W   4   I   5
J   4   G   5   U   5   E   4   R   4
B   4   D   5   Z   3   U   3   P   4
S   3   C   5   R   3   L   3   F   4
N   3   E   4   L   3   J   2   U   2
D   3   O   3   Q   2   Y   1   T   2
Q   2   R   2   V   1   S   1   K   2
X   0   N   2   S   1   Q   1   Y   1
R   0   F   2   M   1   Z   0   X   1
I   0   S   1   Y   0   O   0   N   0
G   0   Y   0   O   0   M   0   L   0
E   0   H   0   F   0   F   0   E   0

Let's analyze the first sub-cipher text to figure out the shift that was applied.

If we order the letter frequencies in alphabetical order and plot them (orange) against the letter frequencies for the English language (black), we see the following:

Obviously, they are out of frame. By inspection, it appears that if we shift the sub-cipher (orange) to the left, we could make them overlap

Indeed, they overlap as well as might be expected.

This shows that the shift used for the first sub-cipher was 7 and therefore the key begins with a G.

Repeating this analysis for the other sub-ciphers, we find the key that was used is

G  H  O  O  N 
7  8 15 15 14

With the key in hand, we can translate the cipher text with the following Mathematica code for Alphabet shifting

ltrs = CharacterRange["A", "Z"];
reorder[str_, n_] := StringReplace[str, #[[1]] -> #[[2]] 
                    & /@ Transpose[{ltrs, ltrs[[Mod[(# + n), 26]]] & /@ Range[26]}]]

mappedSubCiphers = MapThread[reorder, 
                   {StringJoin /@ charactersSample[5], {-7, -8, -15, -15, -14}}
                   ]

which gives a list of the unencrypted sub-plain texts.

We now join them

StringJoin@Flatten@Transpose[Characters /@ mappedSubCiphers]

and present the unencrypted plain text:

MAYEIGHTENIGMAMACHINEBROKENFALLINGBACKONSECONDARYCODESYSTEMSTOPMAYNINEDIVISIONTHREEMOVINGSOUTHTOWARDLEHAVRESTOPMAYTENENEMYNAVALACTIVITYDETECTEDOFFCOASTOFRAMSGATESTOPMAYTENSUSPECTENEMYMAYBEMASSINGFORINVASIONSTOPMAYELEVENWHATISYOURPOSITIONSTOPMAYTWELVEEXTENSIVEENEMYNAVALACTIVITYNEARCALAISSTOPMAYTHIRTEENPLEASEWHATISYOURPOSITIONSTOPMAYFOURTEENINCOMINGSTORMMAYINTERRUPTCOMMUNICATIONSFORSEVERALDAYSSTOPMAYEIGHTEEENMINORSKIRMISHINCHANNELWITHLOSSESONBOTHSIDESSTOPMAYTWENTYDIVISIONTHREEARRIVEDINLEHAVRESTOPMAYTWENTYONEWHATISYOURPOSITIONSTOPMAYTWENTYTWODIVISIONTHREEASSISTINGWITHPREPARATIONSFORBEACHHEADDEFENSESTOPMAYTWENTYNINELACKINGAMMUNITIONFORMACHINEGUNBUNKERSPLEASESENDWITHRESUPPLYSTOPMAYTHIRTYMOREENEMYACTIVITYNEARCALAISMOVINGDIVISIONTHREETOCALAISSTOPJUNEONELEHAVREANDOTHERBEACHESSECUREMASSINGDEFENSEATCALAISSTOPJUNETWOREPORTSOFEXTENSIVETROOPMOVEMENTSANDNAVALACTIVITYOFFENTIRECOASTOFBRITTAINSTOPSUSPECTINVASIONIMMINENTSTOPSENTALLPOSSIBLEREINFORCEMENTSTOCALAISSTOPJUNETHREEALLPOSSIBLEPREPARATIONSCOMPLETEDSTOPJUNEFOURWORRIEDABOUTPOSSIBLEENEMYINTERCEPTIONOFCOMMUNCATIONSSTOPJUNESIXNORMANDYINVADEDSENDHEAVYBOMBREPRISALSTOMANCHESTERONJUNEEIGHTSTOP

Final transmission: JUNESIXNORMANDYINVADEDSENDHEAVYBOMBREPRISALSTOMANCHESTERONJUNEEIGHT

As the last message says, the command is to bomb Manchester, England in response to the invasion at Normandy.

Look for letter patterns and the spacing of the patterns; This will aid in determining key length. Below is a excerpt of that analysis, which clearly shows that the key length is likely 5 letters in length.

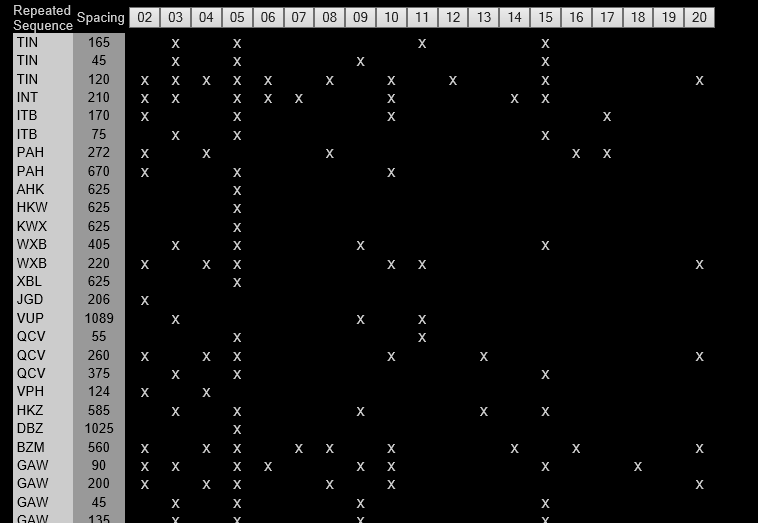
Next, do five separate frequency analysis of every fifth letter (e.g. every fifth letter starting from first letter. Every fifth letter starting from the second letter. etc.) Below is an excerpt of that analysis, which compares the analysis to a standard English language frequency table to determine the shift.

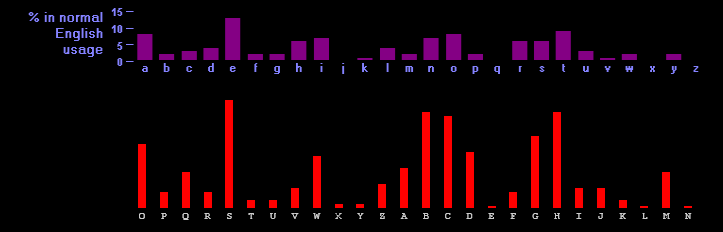
You then can figure out the key word "HIPPO", and decipher the text. The last line of the message reads "...SEND HEAVY BOMB REPRISALS TO MANCHESTER...", and Manchester is the 6th District.

I really like Josh Silverman's solution below with Mathematica!

I used Python. First, I assumed that parts of the coded message might repeat (that is, Kasiski examination.) So I searched for large substrings within the ciphertext that repeat (substring length > 3).

It turns out that HICWUPN repeats at positions 237, 287, 602. AIDD repeats at positions 206, 326, 806, 916, 1066. While GAWE repeats at positions 394, 529, 889.

By inspection, it can be seen that the distance between repeated substrings in each case (287 - 237 = 50; 602 - 287 = 315 etc.) has a gcd of 5. So the key length is probably 5.

Step Two was letter-frequency analysis. Or more precisely, 5 frequency analyses – one for each letter of the key.

To find the first letter of the key, I extracted every fifth letter from the ciphertext, starting at position 0, and performed a frequency analysis on that extracted substring. It turns out the most common letters of that extracted substring are (in descending order) LAHZVUPTKY.

Now all the letters in LAHZVUPTKY are encrypted using the first letter of the key, so if we decode LAHZVUPTKY with the correct first letter of the key, we should get a string containing the most common letters in natural English, with the most common letter first.

There are only 26 possibilities to consider, so this can be done by inspection. We try decoding LAHZVUPTKY using all letters A-Z, and choose the best.

Most results look like a random jumble of letters. If you decode LAHZVUPTKY with the letter Q, for example, we get the result VKRJFEZDUI, which in no way reflects the most common letters in English.

But decoding LAHZVUPTKY with the letter H gives a plausible order of frequent letters: ETASONIMDR. This looks about right; E is the most common letter in English, and TASON are each fairly common. So H is probably the first letter of the key.

We continue with extracted substrings containing every fifth letter, starting at Positions 1,2,3,4. And we discover that the most plausible letters for these letters of the key are I,P,P,O, giving the following letter frequency analyses:

Position 0: LAHZVUPTKY; decrypted with H: ETASONIMDR

Position 1: MQAWIVBZK; decrypted with I: EISOANTRC

Position 2: ITCXHGD; decrypted with P: TENISRO

Position 3: TIPXDCHB; decrypted with P: ETAIONSM

Position 4: SBHCGODW; decrypted with O: ENTOSAPI

And the key is HIPPO.

The way I used to solve is, you need make a frequency table using a programming language of your choice, make a program that allows you to input text and counts how many times (throw them into an array), if you use C++ just use the algorithm standard library, which I prefer not to tell since that's point of the question, right? Compare them to the english letter frequency table, see similarities in the frequency, you can get well, interesting results, although you can improve the program to run a kasiski test (hint hint wink wink, history hint) I used this method. Took me a couple of hours to solve, I also referenced the khan academy video on the caesar cipher, although different its similar what not, I only used coding for frequency analysis. You can learn that the cipher is vulnerable because it can be analyzed, which the worst thing you want as a cipher since it pretty much gives an answer. Another trick is to simply guess out letters in case you don't see a pattern, its close to brute forcing but still reasonable although it only works if you know , say I have the encrypted message I can look at it as three stacks, the plain text on top, key in the middle and encrypted text on bottom. You can throw in common words or simply all the answers converting them through the chart, but its still painstaking without knowing where the answer is so it is unreasonable to use this method, it only works against shorter text. Sorry its a bit lengthy but I hope its some helpful insight on "how" you can get the answer, not "what" the answer is, for the sake of learning.

Here's all the text:

MAY EIGHT ENIGMA MACHINE BROKEN FALLING BACK ON SECONDARY CODE SYSTEM STOP

MAY NINE DIVISION THREE MOVING SOUTH TOWARD LE HAVRE STOP

MAY TEN ENEMY NAVAL ACTIVITY DETECTED OFF COAST OF RAMSGATE STOP

MAY TEN SUSPECT ENEMY MAY BE MASSING FOR INVASION STOP

MAY ELEVEN WHAT IS YOUR POSITION STOP

MAY TWELVE EXTENSIVE ENEMY NAVAL ACTIVITY NEAR CALAIS STOP

MAY THIRTEEN PLEASE WHAT IS YOUR POSITION STOP

MAY FOURTEEN INCOMING STORM MAY INTERRUPT COMMUNICATIONS FOR SEVERAL DAYS STOP

MAY EIGHTEEEN MINOR SKIRMISH IN CHANNEL WITH LOSSES ON BOTH SIDES STOP

MAY TWENTY DIVISION THREE ARRIVED IN LE HAVRE STOP

MAY TWENTY ONE WHAT IS YOUR POSITION STOP

MAY TWENTY TWO DIVISION THREE ASSISTING WITH PREPARATIONS FOR BEACH HEAD DEFENSE STOP

MAY TWENTY NINE LACKING AMMUNITION FOR MACHINE GUN BUNKERS PLEASE SEND WITH RESUPPLY STOP

MAY THIRTY MORE ENEMY ACTIVITY NEAR CALAIS MOVING DIVISION THREE TO CALAIS STOP

JUNE ONE LE HAVRE AND OTHER BEACHES SECURE MASSING DEFENSE AT CALAIS STOP

JUNE TWO REPORTS OF EXTENSIVE TROOP MOVEMENTS AND NAVAL ACTIVITY OFF ENTIRE COAST OF BRITTAIN STOP

SUSPECT INVASION IMMINENT STOP

SENT ALL POSSIBLE REINFORCEMENTS TO CALAIS STOP

JUNE THREE ALL POSSIBLE PREPARATIONS COMPLETED STOP

JUNE FOUR WORRIED ABOUT POSSIBLE ENEMY INTERCEPTION OF COMMUNCATIONS STOP

JUNE SIX NORMANDY INVADED SEND HEAVY BOMB REPRISALS TO MANCHESTER ON JUNE EIGHT STOP