Dividing A Regular Hexagon Into 4 Equal Pieces!
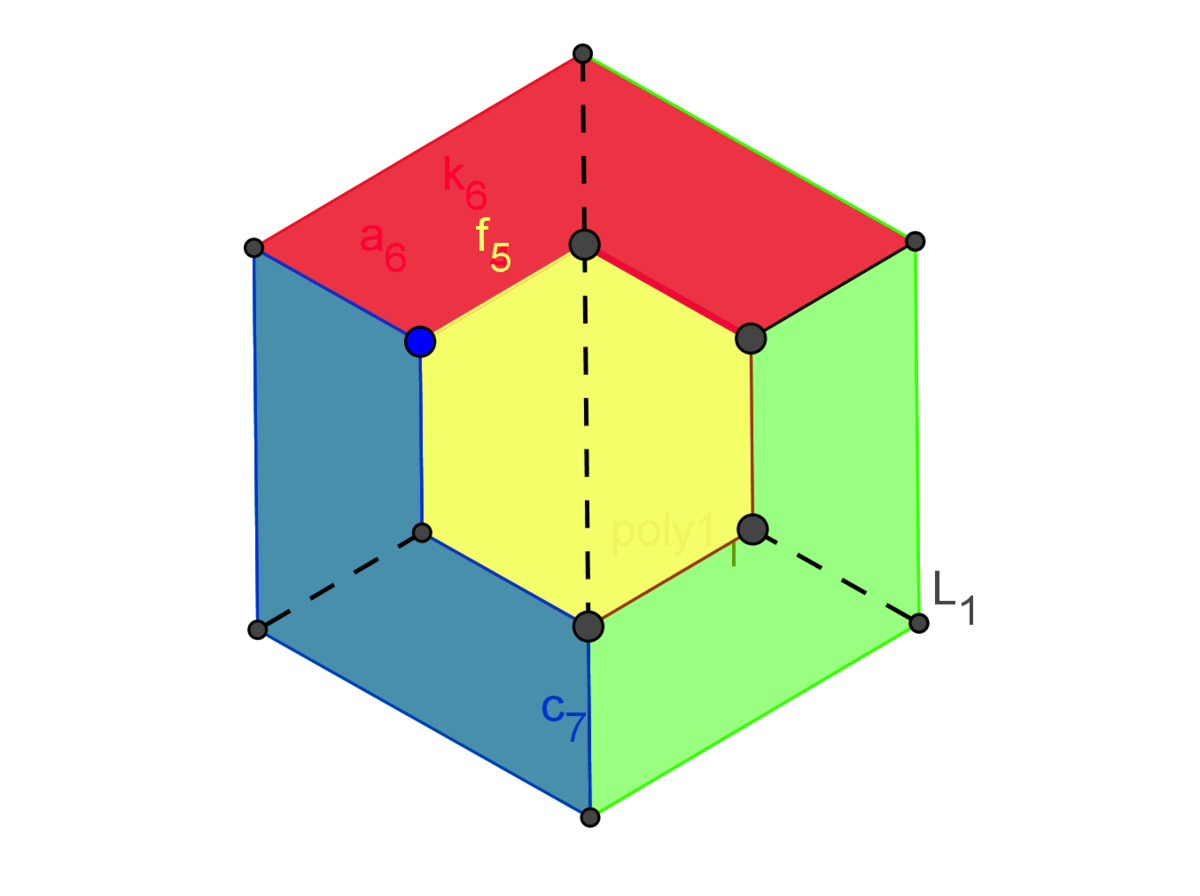
In the diagram above, a yellow regular hexagon lies inside a larger regular hexagon with twice as large a side length.
Each of the 3 line segments connecting the inner and outer hexagons has the same length as a side of the yellow hexagon.
Is it true that the 4 colored regions have the same area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Done in the exact same way :)
Log in to reply
When I am doing problems that way, always tryna to recheck🤣
Based on the given, note that the side of the larger polygon is twice of the side of that of the smaller. And each segment connecting the smaller and the larger polygon, is of the same measurement with that of the side of the smaller polygon. Notice that each region (red, blue, green) is composed of two trapezoid with the same dimensions. Therefore, the area of each region is composed two isosceles trapezoids, with the same corresponding bases (base1 and 2), followed by the same corresponding heights, and that are of the same areas. Thus the area of red, blue, and green regions are the same.
Relevant wiki: Regular Polygons - Area
assume that the length of one side of the bigger hexagon to be 3 units, then the length of one side of the smaller hexagon is 1.5 units
area of the bigger hexagon = 2 2 7 3
area of the smaller hexagon = 8 2 7 3
These values can be found by using the formula of the area of the regular n -gon, A = 4 1 n p 2 cot n π , where p denotes the side length.
difference between the area of the bigger hexagon and smaller hexagon = 8 8 1 3
divide the difference between the area of the bigger hexagon and smaller hexagon by three = 8 8 1 3 ÷ = 8 2 7 3
The 4 colored regions have the same area.
As you can see in the drawing, each colored region has the same amount of squares, so the area will of course be the same. (Sorry for the bad drawing, not to scale)
Let be s the side of the small hexagon. It's area will be (3/2) * sqrt(3) * s^2 (It can be easily computed or found in any math reference, but we only need to see that the area is proportional to s^2 ). So the area of the large, double size, hegagon will be 4 times that of the small one, as seen by replacing s by 2s . So, if we subtract the area of the small hexagon form the area of the large hexagon, we get 3 "parts", i.e. areas, which are equal and each one equal to the size of the small hexagon.
First divide the large hexagon into 6 congruent triangles from the centre to the edge. By the symmetry if the little yellow triangle near the centre is 1/4 of the area of the large triangle then the yellow hexagon must be a quarter of the large hexagon and equal to the other three shaded areas. The area of the large triangle with a base of 2 and a perpendicular of square root of 3 is the square root of 3. The area of the small yellow triangle with a base of 1 and a perpendicular of a half of the square root of 3 is 1/4 of the square root of 3. Hence as the small triangle is 1/4 of the large the small hexagon is 1/4 of the large one. Perpendiculars found using Pythagoras.
A 2D shape scaled up *2 will be 4 times bigger. So we have the original shape as 1/4 and since the other 3 divide the 3/4th of the rest evenly they are all the same
To save ink, let us say that the large hexagon has area 1.
The second paragraph ensures that the yellow hexagon is placed in the centre of the large diagram and so by rotational symmetry the red green and blue areas are all the same.
Since the yellow hexagon has side length 2 1 of the big hexagon, its area is 4 1 .
This leaves an area of 4 3 to be shared among the red green and blue areas. But we have already established that these area are equal, and so each one must be 4 1 just like the little yellow hexagon.
Doubling each side means that the base and the height of the larger hexagon are each doubled. Doubling twice means multiplying by 4. Thus the smaller hexagon is 1/4 the size of the larger.
Extend the three connecting lines to make 3 equal squares. Now we see that the yellow region is made up of 3, quarters of a square. Each of the other regions are 3/4 of a square. They are equal.
Relevant wiki: Regular Polygons - Properties of Regular Hexagons
An area of a regular hexagon is equal to 6 sub-units of equilateral triangles. As shown above, each colored region is composed of 6 equilateral triangles, so they are all equal in area.