Can You Do It?

$Given \quad f(x) + f(\sqrt{1-x^2}) = 2$

$Put \quad x = sin\theta \quad then \quad we \quad see \quad that,$

$f(sin\theta) + f(cos\theta) = 2$

$Now \quad use \quad the \quad same \quad substitution \quad in \quad the \quad Integral \quad to \quad get,$

$\int_{0}^{1} \frac{f(x) dx}{\sqrt{1-x^2}}$

$= \int_{0}^{\pi/2} \frac{f(sin\theta) cos\theta d\theta}{cos\theta}$

$= \int_{0}^{\pi/2} {f(sin\theta) d\theta}$

$Let \quad this \quad be \quad I$

$By \quad properties \quad of \quad definite \quad integral,$

$I = \int_{0}^{\pi/2} {f(sin(\pi/2 - \theta) d\theta}$

$I = \int_{0}^{\pi/2} {f(cos(\theta) d\theta}$

$Thus,$

$2I = \int_{0}^{\pi/2} {f(sin\theta) + f(cos(\theta) d\theta}$

$2I = 2 \int_{0}^{\pi/2} {d\theta}$

$2I = \pi$

$Hence, \quad \int_{0}^{1} \frac{f(x)}{\sqrt{1-x^2}} =\boxed{ \pi/2 }$

Solution as suggested by @shubham dhull

We note that $f(x) =2x^2$ satisfies the condition as:

$\begin{aligned} f(x) +f(\sqrt{1-x^2}) & = 2x^2 + 2\left(\sqrt{1-x^2}\right)^2 = 2\end{aligned}$

Therefore,

$\begin{aligned} \int_0^1 \frac {f(x) } {\sqrt {1-x^2} } dx & = \int_0^1 \frac {2x^2} {\sqrt {1-x^2}} dx & \small \color{#3D99F6}{\text{Let }x = \sin \theta \implies dx = \cos \theta \ d \theta} \\ & = \int_0^{\frac {\pi} {2} } \frac {2\sin^2\theta \cos \theta } {\cos \theta } d\theta \\&= \int_0^{\frac {\pi} {2} } 2\sin^2\theta \space d\theta \\&= \int_0^{\frac {\pi} {2} } \left(1 - \cos(2\theta) \right) \space d\theta \\ & =\left[\theta - \frac {1} {2 } \sin (2 \theta) \right]_0^{\frac {\pi} {2} }\\&=\boxed{\frac{\pi} {2 } } \end{aligned}$

In the integral , directly substitute $x= (1-t^2)^\frac{1}{2}$ . You would see that the integral transforms to 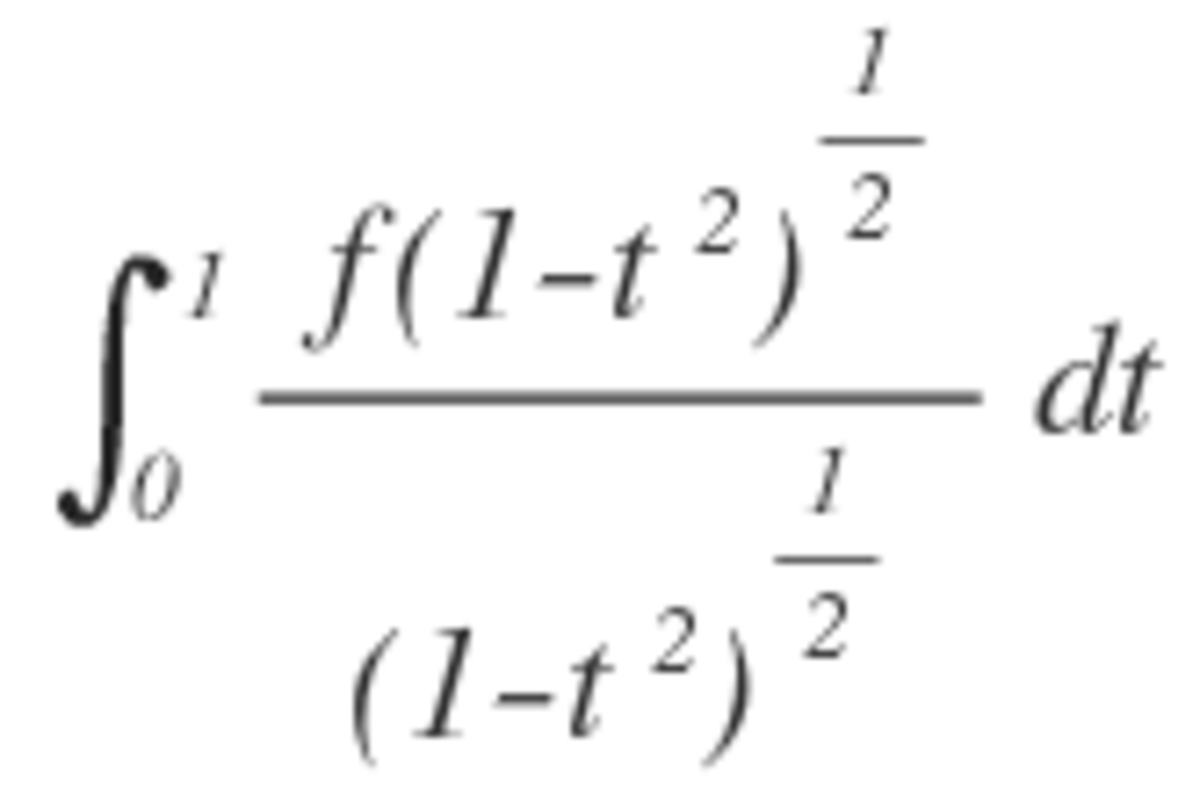Add them to get I = pi/2