Can you draw its graph ? -4

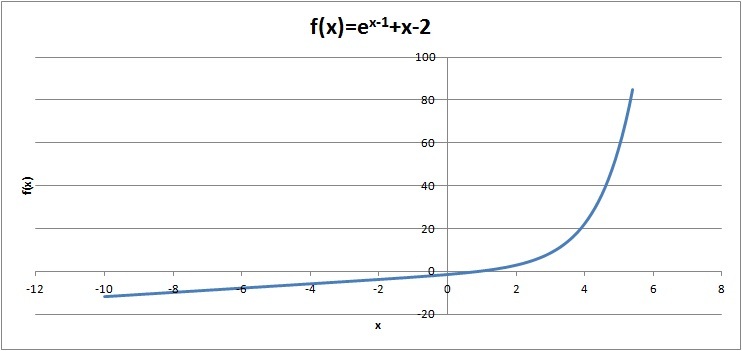
We First notice that $x=1$ solves the problem.

We have $e^{x-1}=2-x$

Now, out of the two functions, represented on the two sides of the equality, we notice that the function on the left hand side , i.e. $f(x)=e^{x-1}$ is a monotonically increasing function, and the function on the rhs i.e $g(x)=2-x$ is a monotonically decreasing function. so, these functions will have common values, i.e. their graph would cut each other, $\text{only ONCE}$ . :D

Since no one gives a graph. I am giving one here.

It is obvious that there is only $\boxed{1}$ real root, when $x =1$ .

e^x/e +x-2=0

e^x+xe=2e

e=2.718

x=2 satisfy

Rewrite it like e^(x-1) = 2-x . Now LHS can be seen as y= e^x/e=.y= ke^x which is an increasing function and y=2-x is clarly a straight line with slope -1. CLEARLY 'ONLY ONE' REAL SOLUTION

as we know e^0=1 so e^0+1-2= 1+1-2= 0

note that value of e=2.71828
power of e if increase i.e x-1>0 then equality never become true(Observation)
power of e if decrease i.e x-1<0 then also equality never become true(Observation).
So check at x=1 which result that equality is true. Hence Only one real solution.