Can you draw its graph-7?

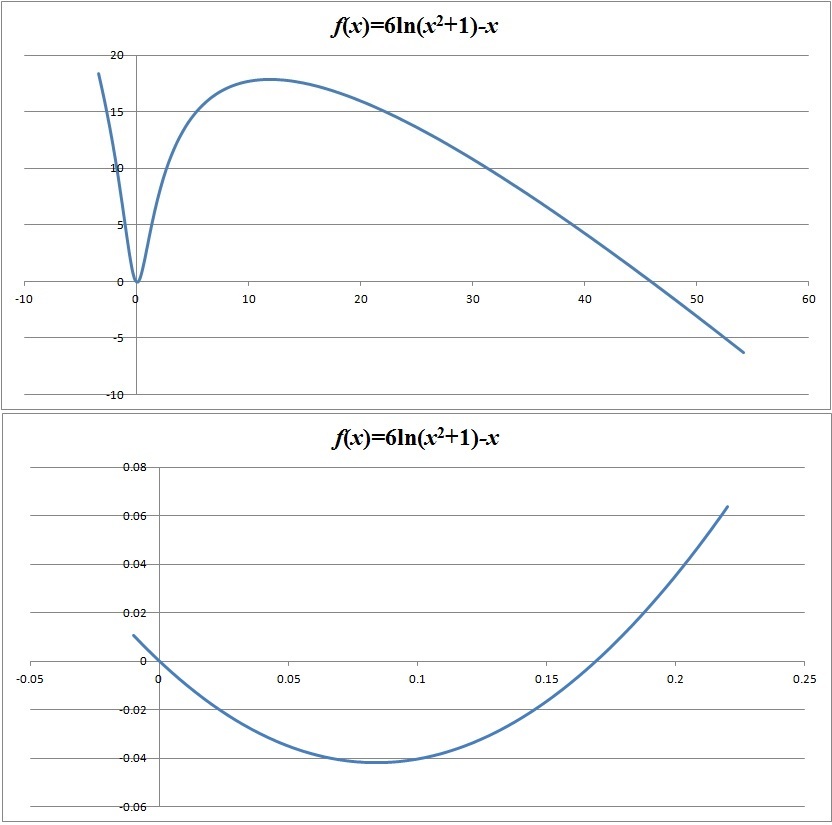
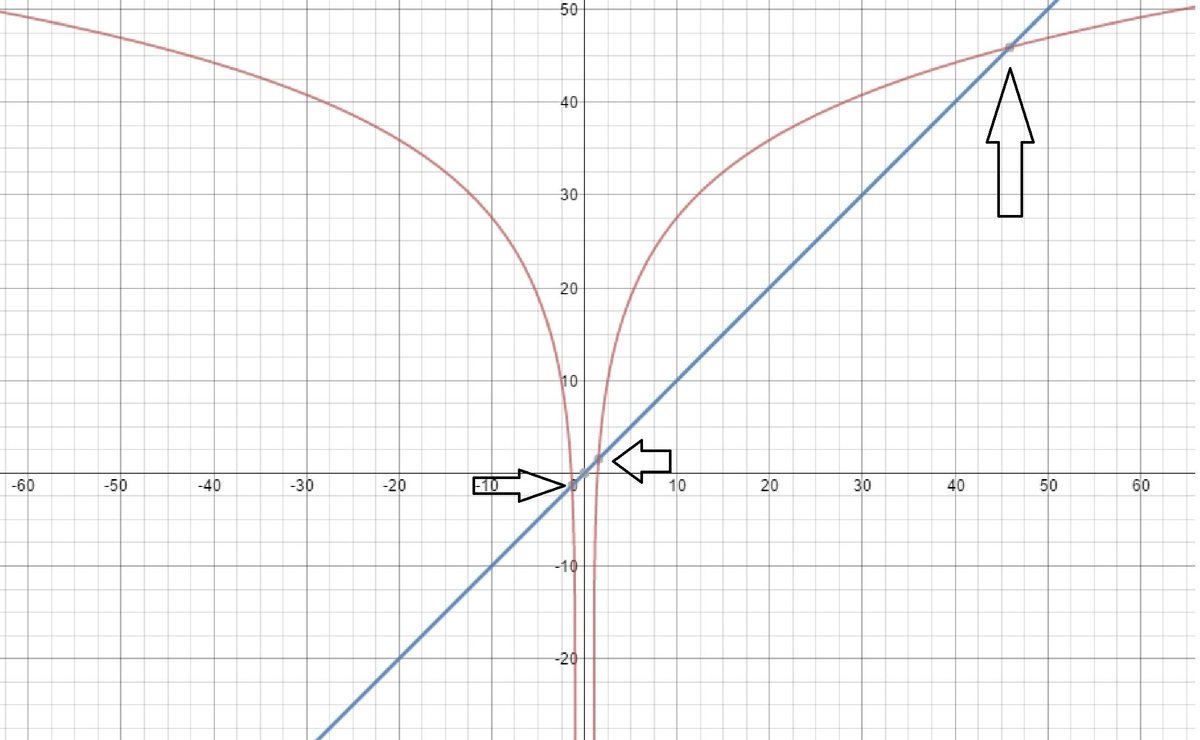
I know solving this problem by graphing is easy, but I'm posting a calculus-based approach anyway.

Let $f(x)=6 \ln {(x^2+1)}-x$ . I don't know what the author means by using the notation $\log$ , so I just assume it's natural logarithm.

Then $f'(x) = \dfrac{{12x}}{{{x^2} + 1}} - 1$

$f'(x) = 0 \Leftrightarrow 12x = {x^2} + 1 \Leftrightarrow x = 6 \pm \sqrt {35}$ .

It is obvious that $f'(x) < 0, \forall x \in (-\infty,6-\sqrt{35})$ so $f(x)$ is strictly decreasing in this interval.

In the same way, it can be concluded that $f(x)$ is strictly increasing in $(6-\sqrt{35},6+\sqrt{35})$ , and strictly decreasing again in $(6+\sqrt{35},+\infty)$ .

Notice that, if $f(x)$ is continuous in the closed interval $[a,b]$ and $f(a)f(b) < 0$ , then there exists some $x_0$ in this interval which is a root of $f(x)$ . Moreover, if $f(x)$ is strictly monotonous in this interval, then $x_0$ is the only root of $f(x)$ in $[a,b]$

$f(-1) > 0$ and $f(6-\sqrt {35}) < 0$ , then $f(x)$ must cross the x-axis exactly once in the interval $(-1,6-\sqrt{35})$ , hence there is one root in this interval (Yes, it's $x = 0$ !).

Apply the same logic for the two remaining intervals, we can prove that the equation has $\boxed {3}$ roots.

From the graph above, we can tell that there are $\boxed{3}$ real solutions. They are $x = \begin{cases} 0 \\ 0.17 \\ 45.9 \end{cases}$