Can you factorise it?
3 x 2 − 1 6 x y + 1 6 y 2 + 1 7 x − 4 4 y + 2 4
If the expression above can be factorized into ( a 1 x + a 2 y + a 3 ) ( a 4 x + a 5 y + a 6 ) with all integer coefficients , what is the highest value of a 1 + a 2 + a 3 + a 4 + a 5 + a 6 ?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Yes mate the whole problem lies on the base that 3 is prime. That gives us the key to this prob..
I believe you have a typo, a 4 = 3 should be a 4 = 1 .
Expression ( 3 x − 4 y + a 3 ) ( x − 4 y + a 6 ) a 3 ( x ) + a 6 ( 3 x ) = 1 7 x a 3 ( − 4 y ) + a 6 ( − 4 y ) = − 4 4 y Solving coefficients 3 x 2 − 1 6 x y + 1 6 y 2 + 1 7 x − 4 4 y + 2 4 = Degree 2 3 x 2 − 1 6 x y + 1 6 y 2 + Degree 1 1 7 x − 4 4 y + 2 4 = ( 3 x 2 − 1 2 x y − 4 x y + 1 6 y 2 ) + ( 1 7 x − 4 4 y + 2 4 ) = ( 3 x ( x − 4 y ) − 4 y ( x − 4 y ) ) + ( 1 7 x − 4 4 y + 2 4 ) = ( 3 x − 4 y ) ( x − 4 y ) + ( 1 7 x − 4 4 y + 2 4 ) = ( 3 x − 4 y ) ( x − 4 y ) + ( 1 7 x − 4 4 y + 2 4 ) Comparing coefficients ⟹ a 3 + 3 a 6 = 1 7 … ( 1 ) ⟹ a 3 + a 6 = 1 1 … ( 2 ) ⟹ a 3 = 8 , a 6 = 3 = ( 3 x − 4 y + 8 ) ( x − 4 y + 3 )
3 − 4 + 8 + 1 − 4 + 3 = 7
There's a typo. In the last third expression of your solution. It should be a6=3.
How do I post an image 😅 I solved the problem but don't know how to post image😅.
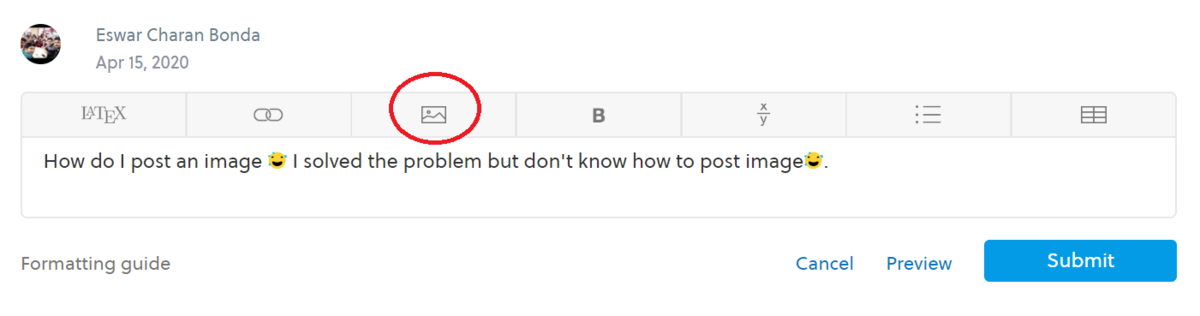
You can use the third button when on editing mode.
Given that ( a 1 x + a 2 y + a 3 ) ( a 4 x + a 5 y + a 6 ) = 3 x 2 − 1 6 x y + 1 6 y 2 + 1 7 x − 4 4 y + 2 4 , equating the coefficients we have:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ a 1 a 4 a 1 a 5 + a 2 a 4 a 2 a 5 a 1 a 6 + a 3 a 4 a 2 a 6 + a 3 a 5 a 3 a 6 = 3 = − 1 6 = 1 6 = 1 7 = − 4 4 = 2 4 . . . ( 1 ) . . . ( 2 ) . . . ( 3 ) . . . ( 4 ) . . . ( 5 ) . . . ( 6 )
With six equations, we can solve the six unknown a k , but it is very tedious. We can just make some educated guesses.
⎩ ⎪ ⎨ ⎪ ⎧ ( 4 ) : 3 a 6 + a 3 ( 5 ) : − 4 a 6 − 4 a 3 a 6 + a 3 = 1 7 = − 4 4 = 1 1 . . . ( 4 a ) . . . ( 5 a ) ⟹ ( 4 a ) − ( 5 a ) : 2 a 6 = 6 ⟹ a 6 = 3 ⟹ a 3 = 8
Therefore a 1 + a 2 + a 3 + a 4 + a 5 + a 6 = 3 − 4 + 8 + 1 − 4 + 3 = 7 .