Can you figure this out (3)!

We have $32+16 = 20+ B$ so $B = \boxed{28}$ . A proof without words or formulas.

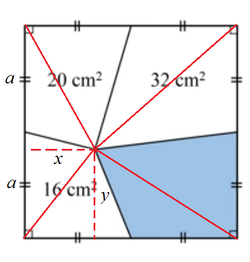
Let the side length of the square be $2a$ and the point where the four internal lines meet be $x$ from the left edge and $y$ from the bottom edge of the square. Then we have:

$\begin{cases} \dfrac {ax}2 + \dfrac {ay}2 = 16 & ...(1) \\ \dfrac {ax}2 + \dfrac {a(2a-y)}2 = 20 & ...(2) \\ \dfrac {a(2a-x)}2 + \dfrac {a(2a-y)}2 = 32 & ...(3) \end{cases}$

We note that the area of the blue region,

$\begin{aligned} A_{\color{#3D99F6}\text{blue}} & = \dfrac {ay}2 + \dfrac {a(2a-x)}2 & \small \color{#3D99F6} \text{which is equal to } (1)-(2) + (3) \\ & = 16-20 + 32 \\ & = \boxed {28}\end{aligned}$

Let the coordinates of A = (0,0), The point where all four lines meet = (x 0, y 0). The length of a side = 2x. After some simplification, we have: 2 16 = x(x_0 + y_0), 2 32 = 4x^2 - x(x 0 + y 0), or 64 = 4x^2 - 32, 4x^2 = 96. But 4x^2 = square area, so ? = 96 - 16 - 20 - 32 = 28. Ed Gray