Can you find BC?
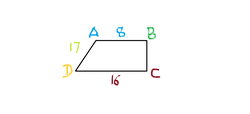 In a given figure,
is a trapezium in which the parallel sides
and
are both
Perpedicular to
. If
,
and
, then
is
In a given figure,
is a trapezium in which the parallel sides
and
are both
Perpedicular to
. If
,
and
, then
is
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
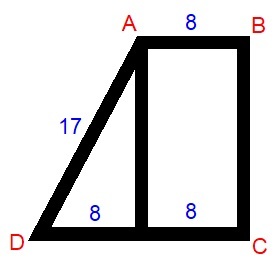
First notice that dc-ab=8 which is equal to the base of the triangle that you can make by drawing an imaginary line on the left of the trapezium. Then use the Pythagorean theorem by doing C^2-A^2=B^2.. 289-64=225 square root of 225 is 15.