Can you find it?
Find the smallest positive integer N such that 1 3 N ≡ 1 ( m o d 2 0 1 3 ) .
Details and Assumptions:
- You may choose to refer to the modulo arithmetic notation.
- 0 is not a positive integer.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
Why must a,b,c be true
Log in to reply
It is the converse of the Chinese remainder theorem
Excellent explanation!!
One thing to note is Euler's Theorem won't necessarily give us the value of the smallest N . So, we shall have find out the smallest value of N manually. We know, 2 0 1 3 = 3 × 1 1 × 6 1 and 1 2 ∣ ( 1 3 N − 1 ) So we aren't concerned about the 3 We know, by Fermat's theorem that 1 3 6 0 ≡ 1 ( m o d 6 1 ) and 1 3 1 0 ≡ 1 ( m o d 1 1 ) But, we wish to find smaller solutions. It is understandable that if it works for a smaller N , then N ∣ 6 0 or N ∣ 1 0 as the case may be. Luckily we get, 1 3 3 ≡ 1 ( m o d 6 1 ) after the first two trials. And for, 1 1 we have, 1 3 N ≡ 2 N ( m o d 1 1 ) After checking for, N = 2 , 5 , 1 0 we get N = 1 0 So, we get our required number i.e. N = 3 × 1 0 = 3 0 Thus, 1 3 3 0 ≡ 1 ( m o d 2 0 1 3 )
$2013=3\cdot 11\cdot 61$
$13\equiv1\pmod 3\implies 13^1\equiv1\pmod 3, N=1$
$13\equiv2\pmod{11}$ and $\phi(11)=11-1=10$ whose divisors are $1,2,5,10$
Now, $2^2=4\not\equiv1\pmod{11}$ and $2^5=32\not\equiv1\implies N=10$
Now, $\phi(61)=61-1=60$ whose divisors are $1,2,3,4,5,6,10,12,15,20,30,60$
$13^1=13\equiv\pmod{61},13^2=169\equiv47, 13^3\equiv47\cdot13\pmod{61}\equiv611\equiv1 implies N=3$
So, N_{min}=lcm$(1,10,3)=30$
Note that we use LaTeX on Brilliant, not TeX.
One thing to note is Euler's Theorem won't necessarily give the smallest n . So we, have to do manually. 2 0 1 3 = 3 ∗ 1 1 ∗ 6 1 and 1 2 ∣ 1 3 N − 1 so we are concerned not about the three. We see by Fermat's Thm. that 1 3 6 0 ≡ 1 ( m o d 6 1 ) , 1 3 1 0 ≡ 1 ( m o d 1 1 ) . But we wish to find smaller solutions. It is understandable that if it works for a smaller n, then n ∣ 6 0 or n ∣ 1 0 as the case may be. Luckily we get 1 3 3 ≡ 1 ( m o d 6 1 ) after the first two trials. And for 11, 1 3 N ≡ 2 N ( m o d 1 1 ) . After checking for n = 2 , 5 , 1 0 , we get n = 1 0 . So, our required number is 3 ∗ 1 0 = 3 0
Implicit in this solution, is that if g cd ( a , m ) = 1 , then there exists a d such that a k ≡ 1 ( m o d n ) if and only if k ≡ 0 ( m o d d ) . Why is this true?
Common mistakes:
-
Most were unable to clearly state the above fact. Saying that "N must be at least 10, N must be at least 3" does not imply that "Hence N must be at least 30".
-
Few solutions clearly showed the value of d for m = 1 1 and m = 6 1 . You can use Euler's Theorem to restrict the values that you have to check.
-
If you claim that 1 3 3 0 − 1 is a multiple of 2013, you will need to provide some justification. Also, explain why no smaller multiple exists.
Factorizing 2 0 1 3 we find 3 ∗ 1 1 ∗ 6 1 .
After that we solve the congruence for each factor:
1 3 a ≡ 1 ( m o d 3 )
1 3 3 b ≡ 1 ( m o d 6 1 )
1 3 1 0 c ≡ 1 ( m o d 1 1 )
{ a , b , c } ∈ N ∗
Knowing that solutions of N must satisfies all the congruences of the factors, we define it by l c m ( a , 3 b , 1 0 c ) .
To get the wanted solution (smallest possible integer), we assume a = b = c = 1 and so we obtain that N = l c m ( 1 , 3 , 1 0 ) = 3 0
Since 2013 = 3 * 11 * 61, we can break down 13^N \equiv 1 \pmod{2013} to : 13^N \equiv 1 \pmod{61}
13^N \equiv 1 \pmod{11}
13^N \equiv 1 \pmod{3}
Now we just the to find the least common multiple of the equations above.
For 13^N \equiv 1 \pmod{61} we try a few N's: N = 0 mod 61 = 1
N = 1 mod 61 = 13 * 1 mod 61 = 13
N = 2 mod 61 = 13 * 13 mod 61 = 47
N = 3 mod 61 = 13 * 47 mod 61 = 1
So N has to be a multiple of 3.
For 13^N \equiv 1 \pmod{11} we try a few N's:
N = 0 mod 11 = 1
N = 1 mod 11 = 2
N = 2 mod 11 = 2 * 2 mod 11 = 4
("by If a \equiv b \pmod{N}, then ka \equiv kb \pmod{N}, where k is a constant", Brilliant Blog) In this case, k = 13^1, since 13 \equiv 2 \pmod{11}, we can multiply it to the next case to find 13^2 \equiv\pmod{11}, 13^3 \equiv \pmod{11}, etc.
N = 3 mod 11 = 4 * 2 mod 11 = 8
N = 4 mod 11 = 8 * 2 mod 11 = 5
N = 5 mod 11 = 5 * 2 mod 11 = 10
N = 6 mod 11 = 10 * 2 mod 11 = 9
N = 7 mod 11 = 9 * 2 mod 11 = 7
N = 8 mod 11 = 7 * 2 mod 11 = 3
N = 9 mod 11 = 3 * 2 mod 11 = 6
N = 10 mod 11 = 6 * 2 mod 11 = 1
So N has to be a multiple of 10.
Lastly, for 13^N \equiv 1 \pmod{3}:
N = 0 mod 3 = 1
N = 1 mod 3 = 1
N = 2 mod 3 = 1
Since 13 = 1 \pmod{3}, we can keep multiplying 13 in for each succeeding case and all of them will be congruent to 1 \pmod{3}.
Therefore, our answer is the least common multiple of 3 and 10, which is 30.
First notice that 2 0 1 3 = 3 ⋅ 1 1 ⋅ 6 1 . By chinese remainder theorem it's enough to solve the equation one factor at a time. For 3 it's always satisfied because 1 3 ≡ 1 ( m o d 3 ) .
For 1 1 we have to solve 1 3 N ≡ 2 N ≡ 1 ( m o d 1 1 ) . Because multiplicative group of integers mod 1 1 has 1 0 elements only 2 , 5 , 1 0 are possibilities. It's easy to see that only 1 0 works because 2 2 ≡ 4 ≡ 1 ( m o d 1 1 ) and 2 5 ≡ 3 2 ≡ − 1 ≡ 1 ( m o d 1 1 ) .
For 6 1 the task is similar only much harder. In theory we'd have to check all of the divisors of 6 0 . Fortunately 3 already works 1 3 3 ≡ 1 6 9 ⋅ 1 3 ≡ 4 7 ⋅ 1 3 ≡ 6 1 1 ≡ 1 ( m o d 6 1 ) and since 2 doesn't work ( 1 3 2 ≡ 4 7 ≡ 1 ( m o d 6 1 ) ), this is the answer (the rest of the divisors being obviously bigger).
Putting it together, the answer is the least common multiple of the solutions found at each factor. That is, 3 ⋅ 1 0 = 3 0 .
How did you get to N^{2} from N^{13} and then to 1 (mod 11) ?
Log in to reply
I think you mean 2 N and 1 3 N . 2 ≡ 1 3 ( m o d 1 1 ) because 1 3 = 1 1 + 2 , so we can replace 1 3 with 2 everywhere. And I didn't really get to 1 , it's just an equation for N that we'd like to solve.
Since 2 0 1 3 = 3 ⋅ 1 1 ⋅ 6 1 , we look at the equation in modulo 3 , modulo 1 1 and modulo 6 1 . Since 1 3 ≡ 1 ( m o d 3 ) , 1 3 N ≡ 1 ( m o d 3 ) for all N . Since 1 3 ≡ 2 ( m o d 1 1 ) , 1 3 N ≡ 2 N ≡ 1 ( m o d 1 1 ) for N ≡ 0 ( m o d 1 0 ) since 2 1 0 = 1 0 2 3 ≡ 1 ( m o d 1 1 ) . 1 3 3 = 2 1 9 7 = 3 6 ⋅ 6 1 + 1 ≡ 1 ( m o d 6 1 ) so taking g cd ( 1 , 1 0 , 3 ) = 3 0 , N = 3 0 .
2013 = 3 11 61
13^3%61 = 1 13^anything%3 = 1 13^10%11 = 1
hence, 3*10 = 30
We first find factors of 2013, i.e. 3 X 61 X 11 Now we observe that 13^N = 1 (mod 3) for any value of N, For 13^N = 1(mod 11) to hold, N has to be at least 10. Similarly, for 13^N = 1(mod 61) is true for N=3.
Hence, minimum value of N=30.
Tools needed to solve the problem:
- Fermat's Little Theorem
- Modulo Arithmetic
1 3 N ≡ 1 ( m o d 2 0 1 3 )
can be expressed as
1 3 N − 1 = 2 0 1 3 k
Since 2 0 1 3 = 3 × 1 1 × 6 1
Then 1 3 N − 1 can is divisible by 3 , 1 1 , 6 1
Let N = 3 k , we have
1 3 3 k − 1 = 3 × 1 1 × 6 1 × k
( 1 3 k − 1 ) ( 1 3 2 k + 1 3 k + 1 ) = 3 × 1 1 × 6 1 × k
By trial and error, I somehow know that 1 3 2 k + 1 3 k + 1 is divisible by 6 1 and 3
Since 1 1 is a prime, by Fermat's Little Theorem we have
1 3 1 0 ≡ 1 ( m o d 1 1 )
Hence, k = 1 0 and N = 3 0
Some flaws in the solution:
-
I can't explain why 1 3 2 k + 1 3 k + 1 is divisible by 6 1 and 3 .
-
I didn't try that N = 3 k immediately when I first saw this problem and I tried N = 4 k instead.
-
I can't really use Chinese Remainder Theorem and Euler's Theorem in this problem. If you know how, please comment or post a solution!
Since we may need a good solution for this problem, I need more suggestion to complete this solution. Hope you all can help!
You have the correct set of tools.
Hint 1:
Show that
1
3
N
≡
1
(
m
o
d
3
)
for all integers
N
.
Hint 2:
Show that
1
3
N
≡
1
(
m
o
d
1
1
)
if and only if
N
≡
0
(
m
o
d
1
0
)
.
Hint 3:
Figure out the case for
1
3
N
≡
1
(
m
o
d
6
1
)
.
Hence conduced that the smallest possible positive integer is N = 3 0 .
import java.io.*;
import java.math.*;
public class CanYouFindIt
{
public static void main(String args[])
{
BigInteger b=new BigInteger("13");
BigInteger v=new BigInteger("2013");
BigInteger k=new BigInteger("2");
boolean c=false;
int i=1;
while(c==false)
{
b=b.multiply(BigInteger.valueOf(13));
k=b.mod(v);
if(k.equals(BigInteger.ONE))
c=true;
i++;
}
System.out.println(i);
}
}
OUTPUT :: 30
i did the same in C++...
Given that 2 0 1 3 = 3 ∗ 1 1 ∗ 1 3 ∗ 6 1 and 1 3 N = 1 ( m o d 2 0 1 3 ) , it must therefore be true that 1 3 N = 1 ( m o d 3 ) = 1 ( m o d 1 1 ) = 1 ( m o d 6 1 )
1 3 = 1 ( m o d 3 ) so therefore 1 3 N = 1 ( m o d 3 ) ∀ N ∈ Z +
1 3 = 2 ( m o d 1 1 ) so:
2 2 = 4 ( m o d 1 1 )
2 3 = 8 ( m o d 1 1 )
2 4 = 5 ( m o d 1 1 )
2 5 = 1 0 ( m o d 1 1 )
2 6 = 9 ( m o d 1 1 )
2 7 = 7 ( m o d 1 1 )
2 8 = 3 ( m o d 1 1 )
2 9 = 6 ( m o d 1 1 )
2 1 0 = 1 ( m o d 1 1 )
Therefore, 1 3 1 0 = 1 ( m o d 1 1 ) and similarly 1 3 N = 1 ( m o d 1 1 ) ∀ N = 1 0 n , n ∈ Z +
1 3 = 1 3 ( m o d 6 1 )
1 3 2 = 4 7 ( m o d 6 1 )
1 3 3 = 1 ( m o d 6 1 )
Therefore 1 3 3 = 1 ( m o d 6 1 ) and so 1 3 N = 1 ( m o d 6 1 ) ∀ N = 3 n , n i n Z +
We now know that N is of the shape 1 0 n and 3 k . Since the L C M ( 1 0 , 3 ) is 3 0 , the smallest value of N such that 1 3 N = 1 ( m o d 2 0 1 3 ) is N = 3 0
For congruence notation you can use a\equiv b \pmod{n} to obtain a ≡ b ( m o d n ) .
Log in to reply
Thank you, tried to find it but I had to type this before a lesson so I didn't have time :(
In the first line you have written 2013=3×11×13×61, please correct it.
2 0 1 3 = 3 ⋅ 1 1 ⋅ 6 1
1 3 N should leave the same remainder, 1 , when divided by 3 , 1 1 , or 6 1 .
1 3 N ≡ 1 N ≡ 1 ( m o d 3 )
This shows us that the prime 3 does not influence the value of N .
1 3 N ≡ 2 N ≡ 1 ( m o d 1 1 )
We need to find the multiplicative order of 2 modulo 1 1 . Fermat's theorem tells us that N "can" be a multiple of 1 0 . We can easily check that, 10 is the smallest solution to the above congruence.
We deduce that N = 1 0 k for some positive integer k .
The last congruence:
1 3 1 0 k ≡ 1 ( m o d 6 1 )
By FLT a possible solution is N = 6 0 , k = 6 , but we do not know that is the minimum or not.
We note that :
1 3 1 0 ≡ ( − 1 4 ) 5 ≡ − 1 4 ⋅ 1 3 2 ≡ 1 3 ( m o d 6 1 )
So, 1 3 1 0 + 1 0 ≡ 1 3 2 ≡ 4 7 ( m o d 6 1 ) , and 1 3 2 0 + 1 0 ≡ 4 7 ⋅ 1 3 ≡ 1 ( m o d 6 1 )
We conclude that N = 3 0 k , which is minimised for k = 1 , and thus the answer is 3 0 .
Although this solution might disgust most of you, it's worth nothing that values of 1 3 N for successive values of N can be cheaply calculated using one of the most basic properties of modular arithmetic. (Calculating them individually is expensive.)

A split-second after launch we see:
169 184 379 901 1648 1294 718 1282 562 1267 367 745 1633 1099 196 535 916 1843 1816 1465 928 1999 1831 1660 1450 733 1477 1084 1 : 30
Doing this with a calculator wouldn't take overly long.
1 2 3 4 5 6 7 |
|
13^n equivalent to 1 mod 2013. It means we have to find the multiple of 2013 which will give the value equivalent to ( 13^n -1).. so we got 30.
Infinite Loop; hopefully there's a solution :)
1 2 3 4 5 6 7 |
|
Since 1 3 N = 1 ( m o d 2 0 1 3 )
We are looking for 1 3 N − 1 = 0 ( m o d 2 0 1 3 )
We know 2 0 1 3 = 3 × 1 1 × 6 1 aand 1 3 N − 1 = ( 1 3 − 1 ) ( 1 3 N − 1 + 1 3 N − 2 + . . . . + 1 )
= 1 2 ( 1 3 N − 1 + 1 3 N − 2 + . . . . + 1 ) . Since 12 is divisible by 3, we have managed to account for divisibility by 3.
Now let's prove divisibility by 11 and 61. We see that 1 3 2 + 1 3 + 1 = 1 8 3 = 3 × 6 1 , so we have another factor of 3 and a factor of 61. The factor of 61 cannot possibly be in 12, it has to be in ( 1 3 N − 1 + 1 3 N − 2 + . . . . + 1 ) and we need 1 3 2 + 1 3 + 1 to be a factor of ( 1 3 N − 1 + 1 3 N − 2 + . . . . + 1 ) so for this to be possible, ( N − 1 ) + 1 has to be divisible by 2 + 1 or rather N has to be divisible by 3 .
We are now left with divisibility by 11. We see that the factor of 11 cannot be in 12, so it HAS to be in ( 1 3 N − 1 + 1 3 N − 2 + . . . . + 1 ) as well. Now 1 3 N − 1 + 1 3 N − 2 + . . . . + 1 = 2 N − 1 + 2 N − 2 + . . . . + 1 ( m o d 1 1 )
= 2 N − 1 ( m o d 1 1 ) . We see that the smallest possible value of N is 10 as we have 2 1 0 − 1 = ( 2 5 − 1 ) ( 2 5 + 1 ) = 3 3 ( 2 5 − 1 ) which is clearly divisible by 11 since 33 is divisible by 11. Hence for 1 3 9 + 1 3 8 + . . . + 1 to be a factor of ( 1 3 N − 1 + 1 3 N − 2 + . . . . + 1 ) , n has to be divisbile by 1 0 too.
We have 3 × 1 0 = 3 0 as our smallest possible value.
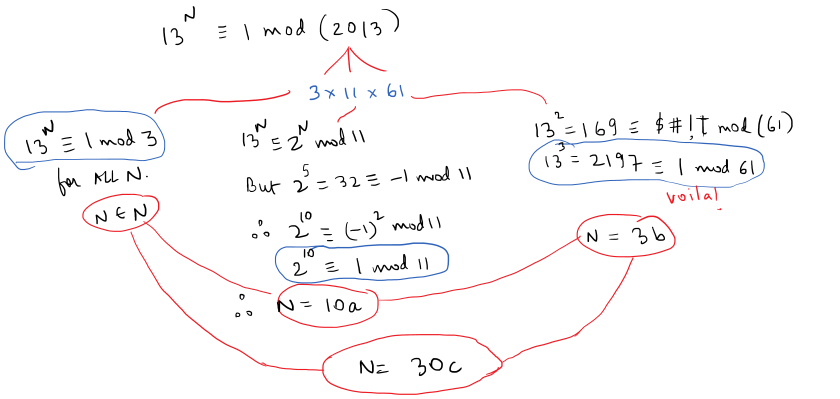
Note that 2 0 1 3 = 3 ⋅ 1 1 ⋅ 6 1 .
This means that 1 3 n ≡ 1 ( m o d 2 0 1 3 ) is true if and only if all of the following are true:
Which values of n satisfy (a)?
1 3 n ≡ 1 n ( m o d 3 )
1 3 n ≡ 1 ( m o d 3 )
Thus, 1 3 n always leaves a remainder of 1 when divided by 3 .
Which values of n satisfy (b)?
Thirteen is the same as two, modulo eleven, so
1 3 n ≡ 2 n ( m o d 1 1 )
Since we're dealing with relatively small numbers here, it's faster to simply list out the powers of two modulo eleven than to resort to more clever methods. Just multiply by two and subtract eleven when necessary. Repeat. Get these numbers:
We can stop since we've found a repeated residue. This means that powers of two (and thus powers of thirteen), modulo eleven, repeat in cycles of 1 0 . In particular,
1 3 n ≡ 1 ( m o d 1 1 ) ⟺ n ≡ 0 ( m o d 1 0 )
Which values of n satisfy (c)?
We do the same thing as above, although this time the multiplication has a danger of being slightly more tedious.
Fortunately, we're done fairly early, with a nice result:
1 3 n ≡ 1 ( m o d 6 1 ) ⟺ n ≡ 0 ( m o d 3 )
We've found (necessary and sufficient) conditions on n so that 1 3 n leaves a remainder of 1 when divided by 3 , 1 1 , and 6 1 , respectively. Thus, 1 3 n ≡ 1 ( m o d 2 0 1 3 ) exactly when all of these conditions are met:
1 3 n ≡ 1 ( m o d 2 0 1 3 ) ⟺ n ≡ 0 ( m o d 1 0 ) , n ≡ 0 ( m o d 3 )
1 3 n ≡ 1 ( m o d 2 0 1 3 ) ⟺ n ≡ 0 ( m o d 3 0 )
The smallest positive integer that is divisible by both 3 and 1 0 is
n = 3 0